Тригонометрични функции, Krugosvet енциклопедия

тригонометрични функции

Тригонометрични функции - един от класовете на елементарни функции.

у функция = COS х.

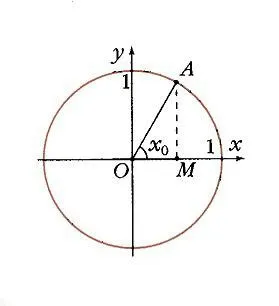
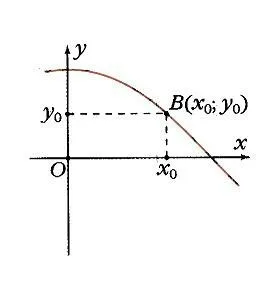
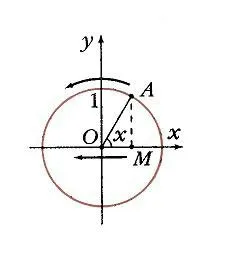
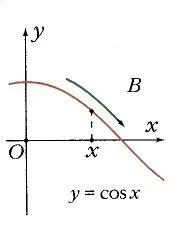
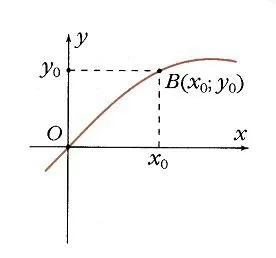
Ако изграждане на единица кръг центриран в основата, и задаване на произволна стойност на аргумента, и се брои от x0 Ox ъгъл ос x0, тогава този ъгъл на единичната окръжност съответства на точка А (фиг. 1) и неговата проекция на оста х е точка М. Дължината на OM сегмента е равна на абсолютната стойност на абсциса точка А. даден x0 стойност е свързан стойност аргумент функция у = защото x0 като абсциса точка А. Съответно точка В (x0; y0) принадлежи към графиката на функция у = COS х (фигура 2). Ако точка А е на правилното оста у, тогава косинус е положителен, ако отляво - отрицателна. Но във всеки случай, точка А не може да напусне кръга. Затова косинус е в интервала от -1 до 1:

-1 = защото х = 1.

Допълнителна въртене на всеки ъгъл кратно на 2 стр. Една точка се връща на едно и също място. Следователно функция у = защото х е периодичен, му период е равно на 2 стр:

Ако вземем две стойности на аргумента, са равни по сила, но с обратен знак, х и -х, намерени на обиколката на съответните точки Ax и брадва. Както се вижда на фиг. 3 на проекцията на оста х е същата точка М. следователно

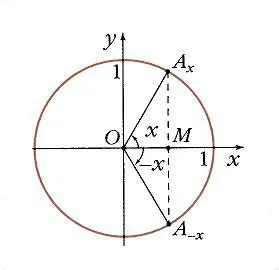
т.е. косинус - дори функция, е (Х) = F (х).

Следователно, възможно е да се изследват свойствата на функция у = COS х в интервала [0, р], и след това се вземат предвид периодичност и паритет.

Когато х = 0, точка А лежи на оста Ox и абсцисата равно на 1, и следователно защото 0 = 1. С увеличаване х точка А се движи по периферията нагоре и наляво, нейната издатина, разбира се, само отляво, и когато X = р / 2 косинус става 0. точка а в този момент се повишава до максималната му височина, а след това продължава да се движи наляво, но намалява. Нейната абсцисата на всички намалява, докато достигне до най-малката стойност, равна на -1, когато х = стр. По този начин, в интервала [0, р] функция у = COS х монотонно намалява от 1 до 1 (фиг. 4, 5).

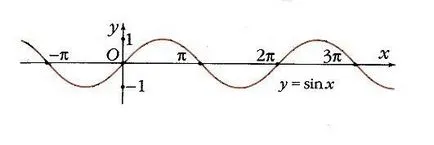
Косинус на паритет означава, че на интервала [- стр. 0] функция нараства монотонно от -1 до 1, като се предполага нулева стойност, при х = - р / 2. Ако вземете няколко периода, се вълнообразна крива (фиг. 6).

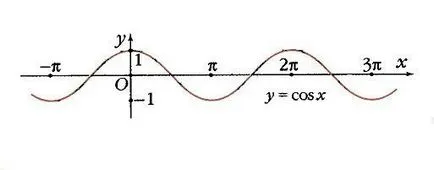
Така функция у = COS х приема стойности от нула при х = р / 2 + к р, където к - е всяко цяло число. Maxima равно на 1, се постигат в точките X = 2k стр. т.е. Етап 2 стр. и най-малко равно на 1, при х = р + 2k стр.

х Функцията у = грях.

На устройството кръг ъгъл x0 съответства на точка А (фиг. 7), и проекция на оста у ще точка Н. функция на затвора W = грях x0 y0 се определя като ординатата на точка А. Точка В (ъгъл x0, y0) принадлежи към графиката на функция у = грях х (фиг. 8). Ясно е, че функция у = грях х периодично, му период е равно на 2 стр:

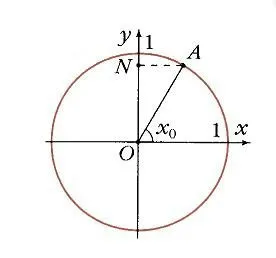
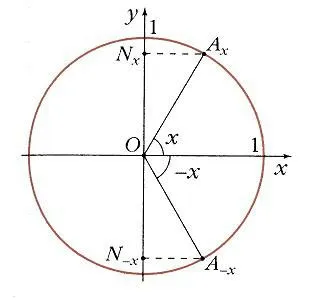
За две аргумент стойности х и - прогнози съответните точки Акс и Ах на оста у разположени симетрично около точката О. Следователно

т.е. задължително - нечетен функция, е (Х) = -f (х) (Фигура 9.).

Ако точката на свой ред А по отношение на точка O до р / 2, на ъгъла на часовниковата стрелка (с други думи, ако ъгъл X да се увеличи с р / 2), а след това да координират своята най-новата позиция е равна на стари абсцисата. Това означава, че

В противен случай, задължително - косинус е "закъснял" на стр / 2, тъй като всяка стойност на косинус на "Repeat" в синусите, когато аргументът се покачва с р / 2. И за да се построи крива на синус, косинус достатъчно смени график при р / 2 надясно (Фиг. 10). Изключително важна особеност се изразява в синуса