Режими на движение на флуиди
В зависимост от вида на течност, скоростта му и естеството на стените, ограждащи потока, има два основни режима на движение: ламинарен и турбулентен. Наречен ламинарен подредени движение, когато отделните слоеве се плъзгат един върху друг, без да се смесват (Фигура ЗА).
режим ламинарен поток може да се наблюдава по-често при вискозни течности, такива като масла, мазнини, и така нататък. Н.
режим турбулентни повикване, в който настъпва случайно движение, когато течни частици се движат по сложен път и слоевете течност непрекъснато се смесват един с друг (фиг. В).
Наличието на два режима на флуидния поток се наблюдават в 1839 и в 1880 Hagen D. I. Mendeleevym.
Достатъчно пълни лабораторни изследвания режими на движение и въпросът за тяхното въздействие върху характера на загубите на налягане на скорост за първи път изучавали английски физик Рейнолдс.
Инсталиране на изследването Рейнолдс на режима течност движение преди появата на сто на фиг. 27. Плавателен съд се напълва с тест течност. Към съд в долната част на стъклената тръба 1 е свързана с крана 2, който регулира скоростта на потока в тръбата. И над кораба е кораб В с разтвор багрило. В отклонява от тръбата на съда 3 с кран 4. край на тръбата 3 се навива в стъклена тръба 1. С цел да попълване на контейнера 5 А е тръба с заключващо устройство 6.
В ламинарен поток движение на флуида в разтвора капене багрило на тръба 1, изтичащи от тръба 3 има ясна видимост на спиралата по дължината на тръбата 1.
Тъй като откриването кран 2 се увеличава и режим на скоростта на движение става турбулентен, на струйка става вълнообразна характер, и в още по-високи скорости напълно ерозирани и се смесва с течността в тръбата. С постепенното затваряне на крана, тези явления възникнат в обратен ред, т.е.. Заменя Е. турбулентни ламинарен.
Експериментите показаха, че преходът от ламинарен за турбулентен поток протича при определена скорост (това се нарича критичната скорост), който е различен за различните течности и диаметъра на тръбата; където критичните скоростта се увеличава с течност вискозитет и с намаляване на тръби с диаметър.
Рейнолдс и няколко други учени са установили, че емпирично знака на режима на шофиране е безразмерна номер, който взема под внимание характеристиките на основния поток
при което - скорост, м / сек; R - хидравличен радиус, m; V - кинематичен вискозитет, m2 / сек.
Това съотношение се нарича числото на Рейнолдс. Стойността на Re, при която турбулентен режим става ламинарен, наречена критична числото на Рейнолдс ReKp.
Ако действителната стойност на Re, изчислена по формула, която да бъде по-голяма от критичната Re> ReKp - турбулентен режим на движение, когато Re За поток налягане в цилиндрични тръби по-удобно да се определи броят на Рейнолдс по отношение на г диаметър, т. Е. където г - диаметър на тръбата. В този случай се оказва, равна ReKp 2300. Ако в формула за тръби с кръгло напречно сечение г изразена по отношение на хидравличния радиус. След това ние се ReKp = 575. За други канали и канали за некръгли напречни сечения могат да се стойността на критичната Рейнолдс броя ReKp = 300 (при изчисляване на хидравличен радиуса в Re). спад на налягането в ламинарен поток Проучванията показват, че с ламинарен поток в кръгла тръба е максималната скорост на оста на тръбата. В стената на тръбата скорост е нула, тъй флуидни частици са покрити с вътрешната повърхност на тръбопровода с тънък неподвижен слой. От стените на тръбата за бързо около оста си увеличава плавно. Графика разпределение скорост над напречното сечение на потока е параболоид на въртене и параболоид аксиален разрез равнина - квадратичен парабола (фигура 4.3).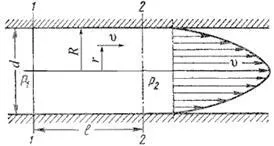
Фигура схема за разглеждане ламинарен поток
Уравнението, свързана променливите # 965; и R, е следното:
при което Р1 и Р2 - налягане съответно в точки 1 и 2.
В тръба стени стойност R = на R. означава скорост # 965; = 0 и когато г = 0 (по оста на потока) скорост е максимална
Сега определи флуидния поток в ламинарен поток в кръгла тръба. Тъй като схемата за разпределение на скорост в кръгла тръба има формата на параболоид на въртене, с максимална стойност на скоростта в тръбата център, скоростта на потока е числено равно на обема на параболоид. Ние дефинираме този обем.
Максимална скорост дава височината на параболоид
Както е известно от геометрията, обемът и областта на височина параболоид з # 961; R2 е
и в нашия случай
Ако вместо R заменен г диаметър на тръбата, с формула (4.4) е под формата
Поток в тръбата може да се изрази чрез средната скорост:
За да се определи загубата на налягане на течността в ламинарен поток в кръгла тръба с дължина L разгледа част на тръбата, на която поток тече под ламинарен режим (фигура 4.3).
загуба на напорен тръбопровод е равен на
Ако динамичен коефициент на вискозитет формула # 956; заменя с кинематичен вискозитет # 965; и плътност # 961; ( # 956; = # 965; # 961; ) И разделят двете страни от обемното тегло на флуида # 947; = # 961; г, получаваме:
От лявата страна на това уравнение е равна на загуби hpot налягане в тръба на постоянен диаметър, накрая това уравнение е под формата:
Уравнението може да се превърне в универсална формула Darcy-Weisbach който накрая се изписва като:
където # 955; - коефициент на триене хидравлично към който поток ламинарен се изчислява по формулата:
Въпреки това, в ламинарен режим за определяне на коефициента на хидравлично триене # 955; TM Basta препоръчва Re <2300 применять формулу
спад на налягането за турбулентен поток течност
Както е посочено по-горе, турбулентен характеристиката на потока на смесване, скорост и налягане пулсации течност. Когато се използва особено чувствителни устройство за измерване на пулсации рекордера, например, скоростта на време при фиксирана точка в потока, получаваме картина, подобна на тази, показана на Фигура 4.4. Скорост на случаен принцип се колебае около стойност средно с течение на времето # 965; OCP, че този случай остава постоянна.
Символи линия тока в тръбата по всяко време е много разнообразен (Fig.4.5).
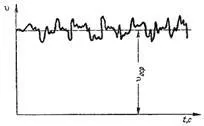
Фигура. Скоростта на пулсация в турбулентен поток. Фигура. Естеството на поточните линии в турбулентен поток
При режима на турбулентен флуиден поток в кривата на разпределение тръба скорост има формата, показан на фигурата в дебелина тънък граничен слой # 948; течността се влива в ламинарен начин, докато останалите слоеве в режима на турбулентен поток и се наричат турбулентен ядро. По този начин, строго погледнато, бурната движение в чист вид не съществува. То е придружено от предложение ламинарен по стените, въпреки слой # 948; режим ламинарен е много малък в сравнение с бурен ядрото.
Фигура. Модел турбулентно движение на течности
Основната формула за изчисляване на загубата на главата в турбулентен флуиден поток в кръгли тръби вече е дадено по-горе емпирична формула, наречена Darcy-Weisbach формула и има следната форма:
Единствената разлика е в стойностите на коефициента на хидравлично триене # 955;. Това съотношение зависи от броя Рейнолдс Re и безразмерна геометрична фактор - относителна грапавост # 916; / г (или # 916 / r0, където R0 - радиус на тръбата).
За първи път бяха дадени най-пълен анализ на определението II Nikuradse, която въз основа на експериментални данни изобразени LG (1000 # 955;) на LG Re продължение на няколко стойности на # 916; / R 0. Nikuradze Експериментите са проведени в епруветки с предварително определена грапавост изкуствено получени чрез поставяне зърна с определен размер на вътрешната стена на тръбопровода. Резултатите от тези изследвания са показани на Фиг. 4.7, когато кривите зависимост LG (1000 # 955) от LG Re за редица стойности # 916 / r0.
Direct Mode I съответства на движението на ламинарен течност.
Освен това, графиката може да се разглежда три области.
Първата област - областта на малкия и Re # 916 / r0, където коефициентът # 955; Тя не зависи от грапавостта, а се определя само от броя Re (линия отбелязани на фигура II). Тази област е хидравлично гладки тръби. Ако номерът на Рейнолдс е в диапазона 4.000 За да се определи има и емпирична формула PK Konakova, който е приложим за хидравлично гладки тръби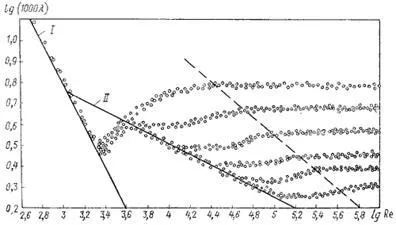
Фигура. График Nikuradze
През втората региона, разположен между редовете II и пунктирана линия в дясно, коефициентът # 955; едновременно това зависи от два параметъра - номер Re и относителната грапавост # 916 / r0, които могат да бъдат заменени от # 916; д. За да се определи съотношението # 955; в тази област може да служи като универсален формула АД Altshul:
където # 916; д - равностойното абсолютни грапавост.
Характерните стойности # 916; е (в mm) за тръби от различни материали са дадени по-долу:
Третата зона - района на високо Re и # 916 / r0, където коефициентът # 955; Тя не зависи от броя Re, определена като относителна грапавост (област вдясно от прекъснатата линия). Този район груби тръби, в които всички линии с различни неравности паралелно. Тази област се нарича режим на самостоятелно домейн или квадратно съпротива, тъй като тук хидравлични загуби са пропорционални на квадрата на скоростта.
дефиниция # 955; за този район произвежда Altshul на опростена формула:
или Prandtl формула - Nikuradze:
По този начин, загубата на налягане, определен от формула Darcy-Weisbach, може да се определи чрез познаването на коефициента на хидравлично съпротивление, който се определя в зависимост от броя Предмет на Рейнолдс и еквивалентната абсолютен грапавост # 916; д. За удобство резюме на определението # 955; са представени в таблицата.
Използвайте, даден в таблицата. 4.1 Формулите за определяне на съотношението # 955; Тя не винаги е удобно. За да се улесни изчисляването, можете да използвате номограмен Colebrook-бял (рисунка), с помощта на които известни и Re # 916; д / г е съвсем просто дефинирано # 955;.
Таблица за определяне на коефициента на хидравлично триене

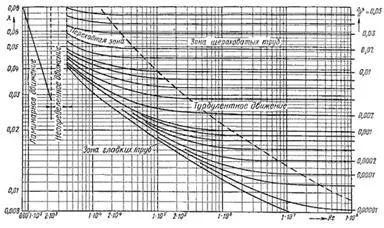
Фигура. Colebrook-Бяла номограма за определяне на коефициента на хидравлично триене
Тестовите въпроси за КЗК:
1.Nazovite основните закони за движението на течности в тръбопроводи
2.Rezhimy движение флуид
3. Стойността на номера на Рейнолдс
4. Опишете Рейнолдс настройка за разследване на режима на движение на флуиди