планарна графика - тя

планарна графика - графиката, което позволява правилното сгъване в равнина (виж колона подреждане.). С други думи, графиката G се нарича. плосък, ако той може да бъде представен в самолета, така че върховете съответстват на различни точки на самолет и ред, съответстващ на краищата (с изключение на крайните си точки) не минават през точките, съответстващи на върховете и не се пресичат. За да се помисли за Хилберт пространство. Намаляване на такива проблеми като проблема за оцветяване карти, проектиране на комуникационни задачи, задачи на електрониката, свързани с прилагането на схемата с помощта на плоски печатни вторични вериги и др. Всяко право (без да пресичат краищата) за свързани Хилберт . създава дял равнина в регионите (повърхности). Този дял се нарича самолета. плосък карта. За всяка карта планарна има формулата на Ойлер където п - брой на върховете, m - броят на ребрата R - броя на картата области (включително външната региона). Оттук графики (пълна графика с п = 5) и (пълна двустранна графика, имащи върхове 3 във всяка част, вж. Фиг. 1) не са плоски. Тези графики са в известен смисъл, минималните непланарните графиките на теоремата Pontryagin - Kuratowski Брой плоски единствено и само ако то не съдържа подграф homeomorphic граф пожар (виж хомеоморфизъм графики.).

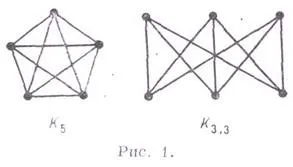
Има и други критерии плоскостността N (т. Е. Свойствата на графиката, за да бъдат плоски). По-специално, графиката Gyavlyaetsya плосък ако и само ако всеки двойно свързан компонент на nontrivial Gobladaet основа на графика такива цикъла, и като допълнителен цикъл Z0. че всеки ръб Gprinadlezhit точно две от М + 1 цикъл (цикли базисни - тази част от графиката цикли, независими и завършване на набор от всички операция допълнение графика спрямо цикъла по модул 2, виж Graf.).

Всяко G. н. Могат да бъдат направени на самолета, така че всички ръбове са прави сегменти линия. Всеки три-свързан CE. (Cm. От графиката) .edinstvennym начин се поставя върху областта (до хомеоморфизъм на сферата). Всяка стифиране Ж. п. Равнината, а оттам и плосък карта, можем да свържем да геометрично двойна графика получава както следва. Във всяка област на картата е поставена но горната част на Хилберт и ако двете области имат общ ръб д, след това се поставя върху тях свързан с ръб д *, пресича само ръб е (Фигура 2 показва твърдите линии Полагане Хилберт и пунктираната ... - неговата двойна графика). Плосък карта. всеки се изправят един рояк е ограничен от три ръба, се нарича. равнинна триангулация. Броят на плоски ръбове на триангулацията с pvershinami равнява 3n - 6.

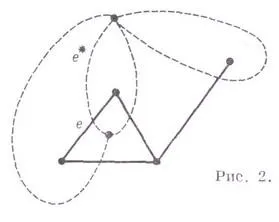
На теория графика, много внимание се обръща оцветители Г. п (виж графика оцветяване.). Nonplanar графика за изследване на различни количествени характеристики, показваща степента на не-плоскостността, например, род, дебелина, размер на графиката, броят на пунктове и т.н. (виж колона опаковка.). ,

Литература [1] Harari Е. Графика теория, транс. от английски език. М. 1973. VB Alekseev.

Енциклопедия по математика. - М. съветски енциклопедия. I. М. Виноградов. 1977-1985.

Вижте това, което "ГРАФИКА плосък" в други речници:

EXTREME ГРАФИКА - графика на ром на един или друг цифров характеристика се минималната или максимална стойност. Обикновено се срещат екстремни стойности на определен числени характеристики на рояк и ограничения върху други числови характеристики и ... ... енциклопедия по математика

ГРАФИКА - много Vvershin и задайте Eneuporyadochennyh и нареди на двойки от върхове; определен чрез G.. Неподреден двойка върхове се нарича. ребро, подреден чифт дъга. G. съдържащ само ръбове, наречен. ненасочена; Г., съдържаща само дъгата ... ... енциклопедия по математика

ГРАФИКА двустранен - ​​bichromatic графика, чиито набор от върха до бодното могат да бъдат разделени в две подгрупи несвързани, и. (Т ... енциклопедия по математика

Плосък графика - графика планарна графика, която може да бъде представена в равнина без преминаване ребра. По-строго: Граф е поставен на повърхността, ако може да се възползва от него, без да преминават ръбове. Laid графика се нарича геометрична му ... Wikipedia

Vertex (графика) - съдържа определения на теория графика. Курсив показват, препратки към условията в речника (на тази страница). # А Б В Г Д Е Ж З И Й К Л М Н О П Р Т U V ... Wikipedia

Планарни графика - равнинна графика графика, която може да бъде представена в равнина без преминаване ребра. По-строго: Граф е поставен на повърхността, ако може да се възползва от него, без да преминават ръбове. Laid графика се нарича геометрична ... Wikipedia

Ламан графика - В графика теория Lamanova графика с п върховете наричат ​​тази графика G, че, от една страна, за всяка к всеки подграф на G, съдържащ к върхове, има не повече от 2k -3 ребра и второ, графиката G е точно 2n -3 ребра. Lamanova графики ... Wikipedia

Речник на теория на графите - съдържа определения на теория на графите. Курсив показват, препратки към условията в речника (на тази страница). # А Б В Г Д Е Ж З И Й К Л М Н О П Р ... Wikipedia

Дължината на диграфа - съдържа определения на теория графика. Курсив показват, препратки към условията в речника (на тази страница). # А Б В Г Д Е Ж З И Й К Л М Н О П Р Т U V ... Wikipedia