Теорията на вероятностите (р

Определение. Факториел на естествено число п е продукт на всички числа между 1 и п, означен с п! = 1 * 2 * 3 * 4 * .... (N-1) * п, в Excel

Пермутации на п обекти се нарича. всеки метод за номериране тези елементи (начина, по който са подредени в един ред).

Броят на пермутации на н предмети равна н!.

= FACT (брой) - връща факторен;

Раздел 8.2 комбинации.

Определение. Ако има N елементи, след което броят на начините, по които можете да изберете точно к от тях е броят на комбинациите от п от к и обозначени

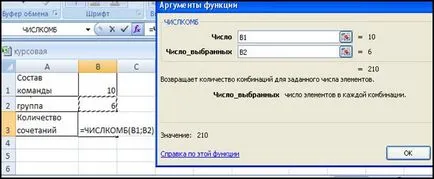
(. N к) = COMBIN - връща броя на комбинациите и се отнася до математически функции;

Пример 1: Колко начини може да бъде избран в началния шест от мача за волейбол, ако отборът се обявява 10 играчи?

Глава 9. Бернули изпитания.

Раздел 9.1. Успех и неуспех.

Тестът се нарича Бернули случаен опит, който може да завърши по един от следните два елементарни събития. Например, никел с монета попада или орел тура до. Стрелецът може да се достигне и може да пропуснете.

Една от двете елементарни събития в тези експерименти е условно наречени успех. а другият - провал.

Вероятността, че опитът е успешен, обикновено обозначени bukvoyr. Вероятността недостатъчност е показан от р. В номера Р и Q са положителни, където р + р = 1

Ако тя е по-равни и независими проучвания Бернули подред, а след това ние казваме, че серия или поредица от Бернули изпитания. Бернули проучвания серия също е случаен експеримент.

Пример 1. симетричен монета хвърлят. Успехът в това преживяване, което наричаме загуба на орел, както и невъзможността - загуба на опашки. . Тъй монетата е симетрична, еднаква вероятност: р = 1/2 и р = 1/2. Когато се провежда серия от 3 хвърляния на монета, вероятността за всеки елементарен случай е равна на 1/8. Изчисляваме, например, вероятността за една елементарна събитие, което има постоянно се появиха орел, опашки и орела. (Успех, късмет и успех). Вероятността от началното събитие Р2 * Q = (1/2) 2 * 1/2 = 1/8 / същия резултат се получава за всички други елементарни събития.

Спор по същия начин, в общия случай, може да се твърди, че по време на серия от п Бернули една елементарна събитие в независими проучвания с вероятност от к успехи

Знаем също така, че броят на елементарните събития с успех, равен на к

Тази формула дава вероятността, че в поредица от п Бернули проучвания дойде точно к успехи, и във всякаква форма. Помислете примерите.

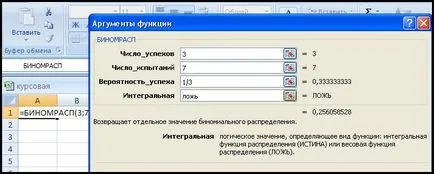
Пример 1. Да предположим, че стреля в целта удари вероятност 1/3. Общо направи 7 изстрела. Каква е вероятността да бъде целта точно 3 пъти?

Този опит - серия от 7 Бернули проучвания с вероятност успех р = 1/3 и вероятността за провал р = 1-1 / 3 = 2/3. Нека събитието A е, че в тази серия дойде точно 3 успех - удари. Ние знаем, че събитието А е предпочитан

елементарни събития. Ние знаем, че вероятността за всеки един от тези елементарни събития: p3q4 = (1/3) * 3 (2/4) 4 = 16/2187

Увеличаването на вероятността от броя на благоприятни събития, ние откриваме, вероятността на дадено събитие А:

Ние реши този проблем с помощта на Excel BINOMDIST (к, п, р, невярно), където к - броят на едно събитие, п - броят на независимите проучвания, стр - вероятността от възникване на събитие, "FALSE" - препратка към това, което се определя от вероятността за точно к събития. В случай, че последният аргумент на функцията е "истинска", функцията връща вероятността, че в н проучвания събитие се случва поне к пъти.

триъгълник на Паскал.

триъгълник на Паскал - аритметична триъгълник, образуван от двучленни коефициентите.

Ако очертанията на триъгълник на Паскал, можете да получите равнобедрен триъгълник. В този триъгълник отгоре или отстрани на разходите за единица продукция. Всяко число е сумата от двете числа над него.