Строителство крива се стича и разделителна способност стрели увисване - проектиране на механична част е
Страница 4 от 37
Изграждане на проводник крива застой и стрели дефиниция увисване
Обща информация. Допустимото напрежение в проводника
Здравината на проводници и кабели с окачване засяга само къси дължини на тел, например, няколко метра дължина между гирлянди анкерни полюси. С дължина на участъци, взети в електропроводи, твърди проводници могат да бъдат пренебрегнати и ги третират като идеални гъвкави нишки суспендират в две точки и се подлагат на равномерно разпределен товар на собственото си тегло на проводника. Тази гъвкава нишка ще очертае линията верига, както е показано на фиг. 2,11 [3, 11, 13].
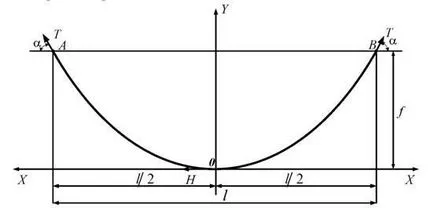
Фиг. 2.11. Curve застой тел на същата височина като точки на окачване.
Както е показано на фиг. 2.11, хоризонталното разстояние между точките на окачване А и В се нарича гредореда и е означена с буквата L. Вертикалното разстояние в средата на участъка между проводниците и правата линия, свързваща AB точката на окачване се нарича провисване и тел стрелката, определена от писмо F. И двете стойности са измерени в метри. Силата навсякъде в проводника и насочени по допирателна към отпуснати крива, наречена садене и е означена с буквата Т. Издърпването най-ниската точка на застой на кривата, насочено хоризонтално, обикновено обозначен с буквата N. Както садене измерени деканютони (Дан) или кг - сила (KGF).
Силата качеството на единица сечение на жицата, наречен напрежение, означена с буквата # 963; и се определя от формулата:
(2.10)
дан / mm. кгс / мм
където Т - в сцепление на проводника, кг (Дан);
F - проводник напречно сечение, мм.
Според [13], изчисляването на механични проводници и кабели, произведени по метода на допустимите напрежения съгласно които е необходимо да се работи в проводници еластичността си материал, т.е. напрежение # 963;, съдържащо се в кабели или кабели, когато
максимален товар удар или най-ниската температура трябва да е по-малка от якостта на опън на проводника материал.
Допустимо максимално натоварване на тел или въже (дан / мм), се определя в зависимост от времето на резистентност тел материал # 963; # 914; (DaN / mm) и получената фактор безопасност п съгласно формулата:
(2.11)
В [13] допустимите напрежения, определени за три първоначални условия: 1) при максимално натоварване; 2) на най-ниската температура; 3) когато средната температура. Стойностите на допустимото напрежение при максимален товар и най-ниската температура, са същите цифрови стойности [13, стр. 324, 325, раздел. 2.5.7].
Определяне провисване тел
Определяне провисване тел с дължина педи по-малко от 800 метра
Ако захранващата линия дължината на въздушната период е по-малко от 800 m, изчисляване провисване проводник произведен от уравнението парабола [3, 11].
За да се извлече уравненията на проводници крива застой поеме координатна система с произхода най-ниската точка на кривата провисване о, X абсциса ос и ординатата ос Y, както е показано на фиг. 2.12.
При извличането на основни уравнения на статиката се използват за системата в равновесие:
а) сумата на проекциите на всички външни сили на осите е равна на нула:
# 931; X = 0; # 931; у = 0; (2.12)
б) сумата от моментите на всички външни сили или техните проекции съответно на всяка точка е равна на нула:
# 931; m = 0 (2.13)
Да разгледаме парче тел, това намаляване на най-ниската точка D и във всяка точка с координатите D (х, у). Частта на рязане на проводника замести съответния сцепление на: най-ниската точка на хлътването на кривата садене Н, и в точка D садене Т.
Тъй като въздушни линии допирателна към хлътването на крива във всяка точка има малък ъгъл с хоризонтална линия, частта на тегло може да се счита за приемане на равномерно разпределено хоризонтално и се заменя с концентриран сила Pi действащ
средата на разглеждания участък, т.е. на разстояние х / 2 от О точки и D, и Tx мощност садене садене сила се равнява на най-ниската точка Н.
Посоката на сила N в точка D е противоположна на посоката на същата дозировка в най-ниската точка на кривата на застой проводници, тъй като поради свойствата на идеално гъвкава нишка може да работи само в напрежение.
В този случай, уравнението на моменти на сили за точка D може да се запише по следния начин:
(2.14)
Решаване на уравнение (2.14) по отношение на Y, ние получаваме основния уравнението на проводник крива застой:
2
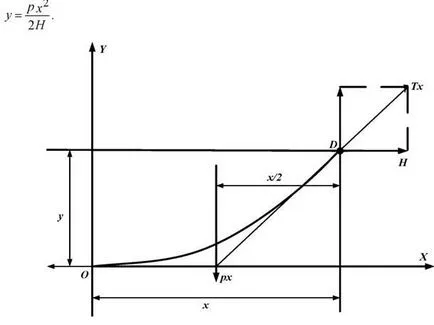
Фиг. 2.12. Външни сили, действащи върху сегмента на тел
Във формула (2,15) включва: единица товар р и сцепление на телта в най-ниската точка на Н. крива провисване не садене В практическо използване същите изчисления като напрежението в проводника # 963; и натоварването на единица, както и спецификата # 947;. Заместването формула (2.15) р = # 947; F и Н = GF. получаваме:
(2.16)
Определяне провисване тел на същата височина на окачване точки
За да се определи хлътването при същите точки височина окачване достатъчно заместени в уравнение (2.16), стойността х = I / 2, тогава
(2.17)
Определяне SAG проводници в различни точки височини окачване
Когато различни височини на точки на окачване проводници провисване крива е асиметрични и най-ниската точка на проводник кривата суров няма да бъде в средата на участъка, и е по-близо до точката А, както е показано на фиг. 2.13, или до точка Б [3, 11].
В този случай е необходимо да се дефинират три различни провисване:
- FC - стрелка огъване в средния диапазон, има експресията, идентичност експресията на хлътването на същата височина като точки на окачване жици формула (2.17);
- еа - стрелка застой тел координира измерени спрямо най-ниската точка на суспензия, се получава от:
- еб - SAG проводници, измерена от най-високата точка на суспензия ордината В, се получава от:
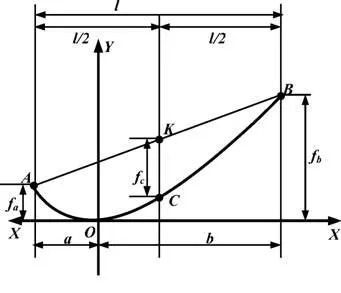
Фиг. 2.13. Curve капещ проводници в различни точки на височина
окачване
Определяне провисване тел с дължина се простира на повече от 800 метра
Когато дължината на участъци над 800 грешка m бум стойности провисване определена от (2.16) надвишава допустимото. В този случай, се използва формулата не получени от уравнението на парабола, и уравнението на контактната мрежа, и определяне на хлътването на биномно формула:
(2.20)
Решението за това дали е допустимо да се пренебрегва втория мандат на формула (2.20), или не, се основава на изчисляването на пропадналия стрели. Ако цифровата стойност на втория срок на формула (2.20) е по-малко от 0,1% от стойността огъване на рамото, е само в този случай може да се пренебрегне.
пример 2.2
Използване на резултатите от Пример 2.1, определя хлътването на AC - 240/32 нормална дизайн за средните годишни работни среди. Жицата е монтиран на стандартен двойна верига свободностоящ стомана поддържа 220 кV.
Начални и обяснения
Според техническите данни (Таблица 2.1.), Се извършва АС-240/32 нормалната структура има напречно сечение алуминиев проводник Fc = 238 mm. и сърцевината стомана - Fc = 43,1 мм. Съотношението на напречните сечения на алуминий и стомана, показва. Според [13, стр. 324, 325, раздел. 2.5.7]
за стомана алуминиеви проводници 120 mm2 или повече, когато m = 6,11-6,25 допустимо напрежение при средна температура # 963; г = 8.7 дан / mm. условия на труд тел Sredneekspluatatsionnye се характеризират с натоварване на проводник # 947 1 = 0,35 · 10-2 дан / mm2 m.
Чрез хипотеза тел проблем е монтиран на стандартен двойна верига свободностоящ стомана поддържа 220 кV. Марка P220-2 опори [6, стр. 40, раздел. 1.34]. За този тип междинни опори участъци са валидни в рамките на L = 470-345 м. Например, да предположим, разтвори 470 m.
решение
Тъй като дължината на междинен период от по-малко от 800 m, проводник бум огъване с формула 2.17, тогава
Определяне SAG проводници, преминаващи въздушни линии на водни прегради и инженерни съоръжения
При проектирането на въздушните линии, необходими за определяне на вертикалното разстояние от кабел към различни кръстосани инженерни съоръжения или водни бариери за да се провери дали наблюдаваната обвивка на допустимото най-ниската точка на кривата на хлабината проводниците до структури или бариери [3, 11, 13, 14]. Типично, в тези случаи е известен само на височината на окачване точки за метални опори (А и В), а височината на най-ниската точка на кривата суров проводник G не е известна. Тъй като местоположението на точка O, която също е произхода не е известен, след като координатна система с произхода на неподвижна точка, например, една от точките за окачване, който е разположен по-горе (точка А на фиг. 2.14). X ос е насочена по посоката на полета, а на ординатата - надолу, успоредни на действието на товара, както е показано на фиг. 2.14.
От височината на окачването точки А и В са различни, както и местоположението на точка O е неизвестен, състоянието на статично равновесие е счупен. В този случай, освен H садене необходимо да се разгледа вертикалната реакция V, успоредна на оста Y, но в посока, обратна него.
Независимо от разликата във височините точки на окачване проводници вертикална реакция зависи от теглото на жицата, равномерно разпределени по цялата си дължина, и е равно на теглото, умножен по половината от дължината на полета:
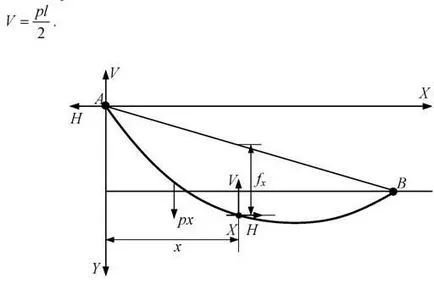
Фигура 2.14. За да се определят координатите на всяка точка по отношение на проводник, получена в горната точка на окачване
Ние образуват уравнение моменти от външните сили, прилагани д произволна точка X координати (х, у) (Фигура 2.14 точката X е в средата на участъка.), С концентрирана сила на собственото си тегло проводници пи действа в средата част:
(2.22)
Желаната стойност в уравнение (2.22) е FX. Решаването това по отношение на желания хлътването, получаваме:
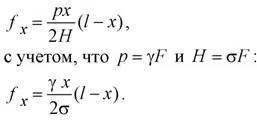
(2.23)
(2.24)
Ако точка В е по-горе точка А, е необходимо да се приемат като точката на произход и промяната в посока Х-ос, това насочване към полета, след уравнението 2.24 остават непроменени.