разтвор производни

За да се разбере определението на производно, помисли следния графиката на функцията.

Фиг.1. Един пример на функция и негово производно.

Гледайки снимката можете да видите местата, където функцията се увеличава бързо, а когато намалява. Например, от гледна точка б до точката графика издига по-бързо, отколкото от точка В до точка С.

Ако преместите точката на графиката на функцията в новата координатна система по такъв начин, че да се повиши точката, намиращ се над оста на х, а на мястото на снижи под х-ос (след скала), и свържете точките, можете да получите нов график за новите функции (долната графика на фиг. 1 ). Тази функция е производно на основната функция. Тази графика не е нищо друго, като показател за степента на функциите на климата. С други думи, производно - функция промяна на скоростта. На практика, производни се използват за определяне на степента на промяна на някои процеси: физически, химически, икономически и т.н.

В по-сложна език, производното - е границата към които съотношението на нарастване на нарастване на х у. Като цяло, функцията производно изглежда и се определя както следва:

Процесът на изчисляване на функцията производно се нарича чрез диференциране.

намерени Функции на практика една голяма част, но има една проста функция (основен), като например, F (х) = sinx, F (х) = C (където C е константа), F (х) = LNX т.н. За тези елементарни функции вече са определени производни, както и достатъчно от тях, за да научите наизуст. Обикновено производни (основни) функции са дадени в таблицата по-долу.

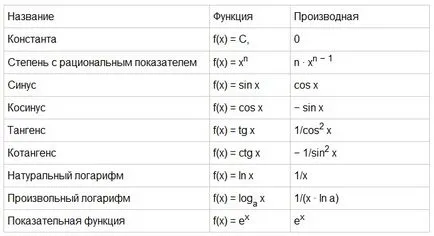
Фиг.2. Таблица прости производни (основни) функции.

Разтвор производни. с прости думи, това е, за да се превърне една функция в друга, вследствие на някои правила (изключение е експоненциална функция F (х) = д ^ х, което не се променя).

Помислете за пример. Необходимо е да се намери на производно на функцията F (X) = х ^ 3 + 3 х ^ 2 - 72x + 90
За решаване на производно е достатъчно да се използва таблицата на производни на прости (елементарни) функции. В съответствие с данните от Таблица получи производното:
F '(х) = (х ^ 3 + 3 х ^ 2 - 72x + 90)' = 3 х ^ 2 + 6x-72

Разтворът на сложна производно

На практика решението на производните на сложни функции трябва да се изправят по-често, отколкото просто.

А правило за определяне на производно на съставна функция, както следва:
(А (б)) '= а "(б) * б", където а-външен функция, б-вътрешна функция.

Необходимо е да се намери на производно на функцията F (х) = греха (3 х-5)

Намерете производната на тази функция, използвайте таблицата на прости (елементарни) функции няма да работят като грях е израз число, т.е. функция се състои от две функции а = грях (х) (външна функция) и В = 3 х-5 (вътрешна функция).

Ние използваме дефиницията на правило на производното на съставна функция и получаване на:
F '(х) = (син (3 х-5))' = COS (3 х-5) * (3x-5) "= 3cos (3 х-5).

Ако материалът е бил полезен otblagorit нашия сайт можете, като направите дарение.
Всяка сума на развитие на проекта, можете да дарите на тази страница.