Рационални и ирационални числа
Ние показахме по-рано, че $ 1 \ frac25 $ - в близост до $ \ sqrt2 $. Ако това е точно равна на $ \ sqrt2 $, проблемът ще бъде решен. След това отношение - $ \ $ Frac, които могат да бъдат превърнати в съотношение от числа $ \ frac75 $, умножаване на горните и долните части на част 5, и това ще бъде неизвестно количество.
За съжаление, $ 1 \ frac25 $ не е точна стойност от $ \ sqrt2 $. По-точен отговор $ 1 \ $ Фрак, ни дава съотношение $ \ Фрак $. Дори и по-голяма точност се постига, когато се равнява на $ \ sqrt2 $ 1 до $ \ Фрак $. В този случай, отношението като цяло число, е равна на $ \ Фрак $. Но $ 1 \ Фрак $ не е точна стойност на корен квадратен от 2. Гръцките математиците са прекарали много време и усилия, за да се изчисли точната стойност на $ \ $ sqrt2, но че те не успяват. Те са били в състояние да предостави съотношение $ \ Фрак $ като съотношение на числа.
Най-накрая големият гръцки математик Евклид се оказа, че без значение колко е повишената точност на изчисленията, за да получите точната стойност на $ \ $ sqrt2 невъзможно. Няма такова фракции, които, когато се издигнат на площада, ще доведат до 2. Тя се казва, че за пръв път стигна до това заключение, като Питагор, но това необяснимо всъщност толкова впечатлен учен, той обеща на себе си и се заклеха с учениците Си, за да запази откритието в тайна , Въпреки това е възможно, тази информация не отговаря на действителността.
Но ако броят $ \ Фрак $ не могат да бъдат представени като съотношение от цели числа, а след това всяка фракция. съдържащ $ \ sqrt2 $, например $ \ Frac $ или $ \ Frac $ също не могат да бъдат представени като съотношение на числа, тъй като всички тези фракции могат да бъдат превърнати в $ \ Frac $, умножена по броя на ден. От $ \ Фрак = \ Фрак \ пъти \ frac12 $. Или $ \ Фрак \ пъти 2 = 2 \ Фрак $, което може да се преобразува, като се умножи горните и долните части на $ \ $ sqrt2, и да получите $ \ Фрак $. (Ние не трябва да забравяме, че без значение какво е номер $ \ $ sqrt2, ако ние го умножете по $ \ sqrt2 $, ние получаваме 2)
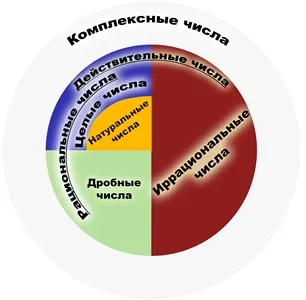
Тъй като броят на $ \ $ sqrt2 не могат да бъдат представени като съотношение от цели числа, то се нарича ирационално число. От друга страна, всички номера, които могат да бъдат представени като съотношение на цели числа се наричат рационални.
Рационално са всички цели числа и фракции, както положителни и отрицателни.
Както се оказа, повечето от квадратните корени са ирационални числа. Рационални квадратни корени имат само номера, включени в броя на квадратни числа. Тези числа се наричат също добра площади. Рационални числа също са една малка част, съставена от тези перфектни квадрати. Например, $ \ SQRT $ е рационално число, като $ \ SQRT = \ Frac = \ frac43 $ 1 или $ \ frac13 $ (4 - е корен квадратен от 16, и 3 - корен квадратен от 9).
Допълнително съдържание:
Сподели с приятели: