Произволен равнина система от сили - studopediya

Под всяка система на силите разбира съвкупността от сили, разположени в една и съща равнина, линията на действие, които не се пресичат в една точка. Произволен самолет система сили може да бъде значително опростена, като приведе власт на една операционна система, за да донесе центъра на резултат в центъра на сила се прилага. нарече главен вектор и тялото като цяло ще бъде прикрепен към един чифт сили МО момент. нарече главен точка спрямо центъра.

Основният вектор е равна на геометричната сума на силите, участващи в системата, а основната точка МО - алгебричната сума от моментите на силите за привеждане в центъра, включително алгебричната сума от моментите на сила двойки:

Цифровата стойност на получения вектор се определя от издатини си върху осите:

Посоката на получения вектор се установи чрез насочване уют на ъгли:

къде. - на единичен вектор на осите говедо Oy.

Условия равновесие тяло под действието на произволна равнина система сили са равни на нула и полученият вектор спрямо основните точки на всеки център О:

са изпълнени, ако Тези условия

Уравнения (1) са наречени основни уравнения на равновесие. Има два други форми на равновесни уравнения:

Системата от уравнения (2) х-ос трябва да е перпендикулярна на линията, минаваща през центъра А и В, и точки А, В и С в системата (3) не лежат на една линия.

Пример С1. (. Фиг С1) твърда конструкция ADSV е фиксирана на опорна точка А панта и в точка Б - подвижен шарнир лагер на ролки. Всички приложими натоварвания и размери са показани на фигурата.

Прилага се от: F = 25 кН, а = 60 °, R = 18 кН, г = 75 °, M = 50 кН х m, б = 30 °, а = 0.5 m Определяне :. реакция в точки А и В, причинена от товара.

Решение. 1. Помислете за баланса на рамката. Начертайте XY оси и привлече в качеството на рамката на власт: сила. сила двойка на въртящ момент М, кабелна напрежение (модул T = P) и свързва реакция. , (Реакция на фиксирана ос лагер изобразяват две от нейните съставки, ролки за подпомагане на реакцията шарнирни е перпендикулярна на референтната равнина).

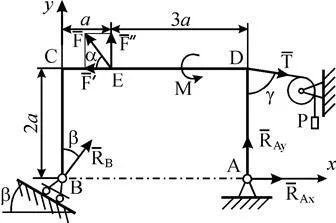
2. За получава плоска форма системата три сила на равновесие уравнения. При изчисляването на момента на сила около точката Avospolzuemsya Pierre Varignon теорема, т. Е. Разширяване на сила в компоненти. () И да вземе предвид това. получаваме:

От уравнение (6) намираме:

Marks показват, че реакцията и противоположна посока е показано на фигурата.

За да проверят верността на резултатите и да реши да изготви проверка уравнение на равновесие във формата на моменти на всички сили за точка В.

Пример С2. Конструкцията се състои от твърд гон AEC SK прът и че в точка С (фиг. C2a), свързани един с друг чрез цилиндричния шарнир.

Външни връзки са в точка А - панта-неподвижна опора, в точка Б - BB безтегловност прът ¢, в точка D - осово-подвижния супорт. За дизайна се прилага сила. двойка сили с момент М и равномерно разпределен в района на HF интензитет товар Q на.

Прилага се от: F = 10 кН, а = 60 °, р = 20 кН / m, M = 50 кН х м, = 0.5 m.

Определя реакции ограничаващите в точки А, В, С и D, поради предварително определен товар.

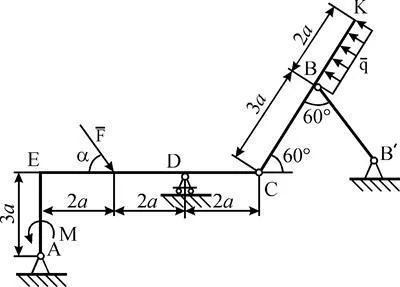
Решение. 1. За да се определи реакционната система разчленено от панта С и се считат първия вал баланс CS (фиг. S2B). Начертайте XY оси и привлече в качеството на сила прът: равномерно разпределен товар замени сила. прилага в средната част на ВХ (числено Q = Q х 2а = 20 кН), реакционният прът BB ¢ насочена по пръта, и действието изхвърля гон AEC представляват компоненти и реакционната панта В.

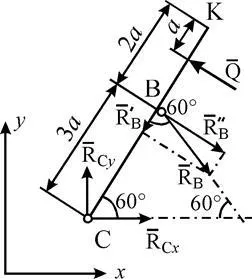
За да се получи равна система сили е три равновесни уравнения:

При изчисляване на момента на сила го разлага на компоненти и употреба, както и Пиер Varignon теорема (.).

От уравнение (9) намираме

2. А сега да разгледаме баланса на полигона (фиг. C2b).

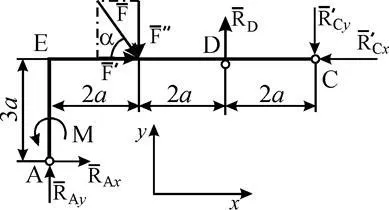
Акт върху него: сила. двойка на сили с момента М, реакцията на осово-подвижния супорт D, компоненти и реакционната осово неподвижна опора А и компонентите и реакции. насочено срещу съответните реакции и. които са прикрепени към пръта на COP. Когато решения се отчита, че числено = и =. от гледна точка на равнопоставеността на действие и реакция. За този плосък система сили, също имаме три равновесни уравнения:

В уравнение (12) за изчисляване на момент на сила. последният разбива на компоненти и теорема (II) и се прилага Varignon му.

От уравнение (12) намираме:

От уравнение (10):

От уравнение (11):