Намери интервали от увеличаване и намаляване на деривативни функции в ПТ

\ (\ Blacktriangleright \) Ако производното е положителен, в интервал \ на ((а, б) \). на това функцията е строго увеличава. \ (F '(х)> 0 \ Longrightarrow е (х) \ uparrow \)

Ако производното е отрицателен в интервал \ на ((а, б) \). на това функцията е строго намаляваща. \ (F '(х)<0 \Longrightarrow f(x) \downarrow\)

Имайте предвид, че обратното не е вярно. Това означава, че ако функцията е строго повишаване на някои интервал, а след това не следва, че всичко на този период на нейната производна е положителна. Например:

функция \ (е (х) = х ^ 3 \) в интервал \ на ([- 1; 1] \) е строго нараства, но производно не е положителен навсякъде: в \ (х = 0 \) негово производно \ (F ' (0) = 0 \) (както \ (F '(х) = 3 х ^ 2 \)).

\ (\ Blacktriangleright \) Ако функцията не намалява (увеличение и / или постоянен) в интервал \ на ((а, б) \). след това този интервал негово производно е неотрицателно (\ (\ GEQ 0 \)). Обратното е вярно.

\ (\ Blacktriangleright \) Ако функцията е nonincreasing (намалява и / или постоянни) в интервал \ на ((а, б) \). след това този интервал негово производно не е положителен (\ (\ екв 0 \)). Обратното е вярно.

\ (\ Blacktriangleright \) в точките на фрактура (на фигурата тази точка \ (А \) и \ (B \)) производно не съществува.

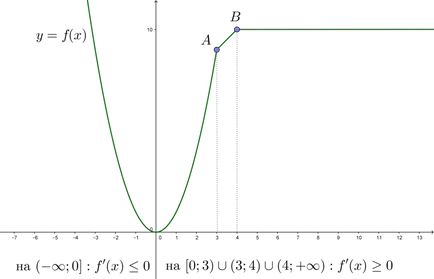
Имайте предвид, че интервал \ на ((4 + \ infty) \) производно \ (F '(х) = 0 \). защото в този интервал е постоянна функция (\ (е (х) = 10 \)).

Пример: получите брой точки, при което производното е равна на нула, ако стойността е графика функции:

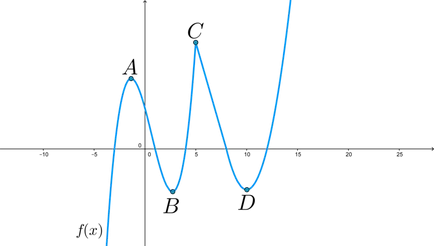
Производното е нула в точките \ (А, В, D \). и в точка \ (С \) не съществува, тъй като е точката на счупване.

Заключителни работи под формата на ЕГЕ за 11 клас задължително да съдържа референция за изчисляване на сроковете и намаляване на пропуските за увеличаване на функцията производно, търсенето на екстремум точки и заговор. Добро познаване на темата дава възможност да се отговори правилно на няколко тестови въпроси и не изпитват трудности при по-нататъшно професионално обучение.

Основи на диференциално смятане - една от основните теми на съвременната математическа гимназия. Тя се изучава използването на производни за изследване на зависимата променлива - е производно може да бъде анализирана увеличаване и намаляване функция без позоваване на чертежа.

Комплекс подготовка на завършилите да преминат изпит по образователен портал "Shkolkovo" дълбоко ще разберат принципите на диференциация - подробно да се разбере теорията за проучване на примери за решаване на общи задачи и да се опита ръката си в самостоятелна работа. Ние можем да ви помогне да запълни празнините в знанията - да се изясни понятието лексикални понятия и теми за зависими променливи. Учениците ще имат възможност да се повтаря как да намерите монотонността интервали, което означава, покачването или намаляването на функцията производно на определен интервал, когато крайни точки са включени и не са включени в интервалите на резултатите.

Изборът на раздел "строителя", студентите ще могат да практикуват в изследването на увеличаване и намаляване на производна функция на версиите на недвижими изпит постоянно се актуализира, за да се отразят последните промени и нововъведения.