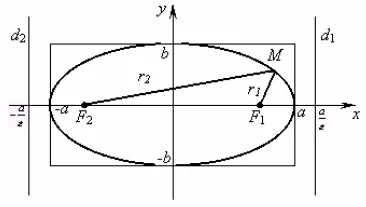
Ellipse и нейното канонично уравнение

Определение 3.5.2. Ellipse е множеството от всички точки в равнината, сумата от
разстоянията, от които до две точки за данни на тази плоскост, наречени фокуси, има
постоянна стойност равна 2а.
В каноничен уравнението на елипсата е дадено от

където - голяма полуос; б - малка ос. Точки F1 (с, 0) и F2 (-С, 0) - в наречен
огнища на елипсата, формата на елипса (мярка за неговото сгъстяване) се характеризира със своята
ексцентричност
Определение 3.5.3. радиус Focal е разстоянието от кривата до точката на фокус.
Focal елипса радиуси R1 и R2 са свързани с
С елипсата е свързано с две големи линии, наречени негови directrices d1 и
d2. чиито уравнения са на формата. Съотношението на разстоянието от всяка точка на елипсата
да се съсредоточи на разстоянието, съответстващо на ексцентричността на елипсата е равна на направляващата # 949;.

Специален случай на елипса уравнението когато уравнението е окръжност с център в точка О (0,0) и радиус. В каноничен уравнението на окръжност с
център в точка О "(а, Ь) и радиус R е дадено.
Други канонично уравнение на елиптични криви:
Уравнение 1 определя точка O (0,0);
Уравнение 2 уточнява въображаем елипса;
3. уравнение определя въображаемата окръжност.