Еквивалентно елементарен матрица трансформация и

Елементен трансформация на редовете на матриците се наричат ​​редове следните трансформации:

1. ред умножаване с ненулева число;

2. прегрупирането на две линии;

3. Добавянето на един ред от другите линии, умножена по не-нулево число.

Ако матрицата на матрица от палци използване еквивалент трансформация на редовете, матриците са еквивалентни и представляват.

Примери на елементарни трансформации,

Покажете на всички елементарни матрици превръщат примера

Размножава първия ред на матрицата на две, т.е., всеки елемент на първия ред се умножава по две, ние получаваме матрица резултат. еквивалентни на дадена матрица:

Промяна на първия и втория ред на матрицата, получаваме еквивалентно матрица:

От първия ред на матрицата изваждане на втория ред, ще получим еквивалент матрицата:

В резултат на това можем да заключим, че матрицата и равностойността като на един от тях се приближи до другия чрез еквивалентни преобразувания на редовете.

Кронекер - Капели

Системата на линейни уравнения е съвместима единствено и само ако ранга на основната му матрица е равен на ранга на своя разширената матрица, със системата има уникално решение, ако в ранг е равен на броя на неизвестни и безкраен брой решения, ако ранг е по-малко от броя на неизвестни.

Комплексни числа. Събиране и умножение

Комплекс [1] (остарели имагинерно число. [2]) - брой видове. където - реални числа - имагинерната единица (стойността, за която равенството :). Множеството от всички комплексни числа с аритметични операции е поле и обикновено се означава с латински. комплекс - са тясно свързани.

Това означава, че (две комплексни числа са равни, ако и само ако те са реални и въображаеми части).

25) Ако. тогава броят се нарича комплекс конюгат на номера.

Това означава, че сложните спрегнати номерата на реални части са равни и различни въображаеми знак.

Например. Комплексът конюгат на броя е броят.

На комплексната равнина на сложни спрегнати числа, получени огледални образи един на друг по отношение на реалната ос.

Свойства на комплексни числа спрегнати

1) Ако. може да се заключи, че броят считат за валидни.

2) За всяко комплексно число сума - действителния брой.

Например. Да. след това. и след това

3) За произволно комплексно число продукт.

Например. Да. сложни конюгат номера. След това продуктът

4) Модулите на комплексни числа конюгатни са равни. и аргументите са различни знак (фиг. 1).

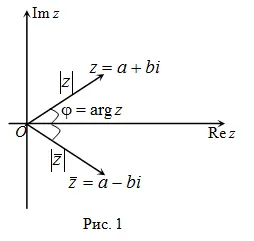
9) Ако - комплексни конюгатни номера, след това