Медиана - на снимката 7312-6
<<Из точки, не лежащей на прямой, можно провести перпендикуляр к этой
Медиана триъгълник >>
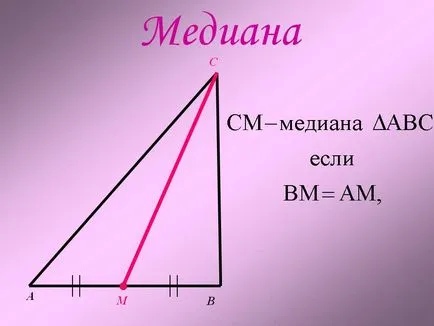
Медиана. SA MV
Снимка 6 от представяне "Четири триъгълник център" за урок геометрия на тема "Триъгълник"
Размер: 960 х 720 пиксела, на формат: JPG. За да изтеглите картинката за урок по геометрия, кликнете върху снимката на десния бутон на мишката и изберете "Save Image As. ". За да покажете изображения в класната стая, можете да изтеглите безплатно представянето на "Четири Велик момент treugolnika.ppt" изцяло с всички снимки в цип архив. размер на файла - 83 KB.
триъгълник
"Видове триъгълници» - Б. Учителят по математика и геометрия Плеханов Анастасия Nikolaevna. Видове триъгълници. Точките се наричат върхове и otrezki- страни.
"Посрещане на предизвикателствата» - AO: OC = BO: OD. Помислете за решаването на медианите на триъгълник имота. задачи на готови решения чертежи. Урок Цели: Да се въведе определение на средната линия на триъгълника. Членка и да се докаже теоремата на средната линия на триъгълника. Резултатите от домашното урока. Изследване на нов материал. В хода на урока. Докажете, че MN || AC.
"Историята на Питагоровата теорема" - и всеки построени катетри квадрат, съдържащи два триъгълника. През вековете е давани много доказателства за Питагоровата теорема. Щедро е жертва на боговете на Питагор. Исторически преглед ще започне с древен Китай. Задача №1. И в освобождението на душата на целия подход, с отражения.
"Решението на триъгълници 9 клас» - у. Геометрия, 9 клас KM: "Отношенията между двете страни и ъгли на триъгълник". 1. Дайте определение за грях. защото. 2. Що се промени: грях. защото. Решение правоъгълен триъгълник. дали греха на ценности зависи. защото. радиусът на кръга? W. Uz 2: площ на триъгълника в тригонометрични форма S? =. а б грях С,
"Медиана триъгълник" - Помислете площада. BHD и? SKD. Не. Какво знаеш за медианите на триъгълника? Триъгълниците са на крак и малък ъгъл. Ако са медиани, които разделят триъгълника на 6 равни по размер триъгълници. Въпрос: Има ли нужда от гледна точка на равенството на всички шест области на триъгълници? Нека да докаже обратното.
Само на "триъгълник" 42 презентации