Двойствеността в линейното програмиране

Основни понятия от теорията на двойственост.

Всеки линейното програмиране проблем може да се свърже с друг линейното програмиране проблем. В решаването на един от тях, автоматично ще бъде решен още един проблем. Тези задачи се наричат vzaimodvoystvennymi. Ние показваме как на този проблем (ще го наричаме оригинала), за да се изгради своя двоен.

Да разгледаме проблема на планираната за производство.

Съдържанието на състава на директен проблем. такъв план, изход X = (x1, x2. хп), в който печалбата (приходи) от продажби на продукция е максимумът, при условие, че консумацията на ресурсите на всеки продукт трябва да надвишава наличните резерви.

Общи правила за съставяне на двоен проблем.

Обективната функция (мин)

В дясната част на ограничения

Обективната функция (макс)

А - ограничение матрица

A T - ограничение матрица

аз-ти ограничение: ≥ 0, (≤ 0)

променлива ил ≥ 0, (≤ 0)

аз-ти ограничение на: 0 =

≠ Променливата ил 0

Променлива XJ ≥ 0

J-ти ограничение: ≤ 0

Променлива XJ ≠ 0

J-ти ограничение: 0 =

Ние се изгради своята двойна задача на следната правила.

Броят на променливи в двоен проблем е броят на неравенството по отношение на оригинала.
Матрицата на коефициент на двойния проблем е транспонирана към първоначалните коефициенти на матрицата.
Колона на свободните отношение на първоначалния проблем е низ от коефициенти за целевата функция на изделията с двойна употреба. Целевата функция е минимизиран в една задача към друга е сведена до минимум.
Условията на не-негативност на означенията съответстват на първоначалния проблем, двойните ограничения на неравенство, насочен в далечния. Обратно, неравенството, ограниченията в оригиналната съответстват на условията на не-неотрицателност в двойната.

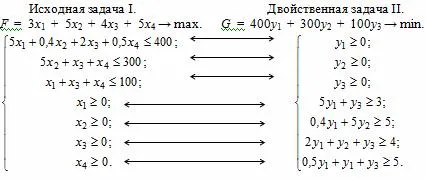
Имайте предвид, че задачата ми реда колони на матрицата са проблеми II. Следователно коефициентите на променливите в проблем у, II - са съответно коефициентите на аз-ти неравенство проблем I.
Полученият модел е икономическата и математическия модел на проблема с двойна към директния проблема.

За да се построи двойна проблем използването на тази услуга

Неравенства са свързани със стрелки, са конюгат.
Съществена производство на двойна проблема. намиране на определена цена (оценки) ресурси Y = (y1. y2. хм), в която общата стойност на средствата ще бъде минимално, при условие че стойността на ресурсите в производството на всеки продукт ще бъде не по-малко от печалбата (приходи) от продажби на тези продукти.
цени y1 ресурс. v2. хм в икономическата литература сме получили различни имена: регистрация, имплицитно, сянка. Смисълът на тези имена е, че тя е обвързана с условието, "не истински" цени. За разлика от "външни" цени C1. s2. Известно КН на продукта, като правило, преди началото на производствените цени Y1 ресурси. v2. хм са вътрешни, защото те са определени, не е от външната страна, но се определят като пряк резултат от решаването на проблема, така че те често се наричат разчети на средствата.
Съобщение първична и двойна проблеми е, по-специално, че решението на един от тях може да се получи директно от други решения.

Duality теореми

Двойствеността е основно понятие в теорията на линейното програмиране. Основните резултати от теорията на двойственост затворени в две теореми, наречени Duality теореми.

Първо двойственост теорема.

Ако една от чифт двойна проблеми I и II е решим, е решими и от друга страна, с обективната функция в оптимални планове съвпадат, F (х *) = G (у *), където X * Y * - оптимални решения I и II

Вторият двойственост теорема.

План на Х * и Y * са оптимални в проблеми I и II, ако и само ако за тях заместване в рестрикционни задачи I и II, съответно, най-малко един от всеки чифт конюгат неравенства става равенство.
Това е основната двойственост теорема. С други думи, ако х * и Y * - приемливи разтвори първични и двойна проблеми и ако в Т х * = б Т у *, тогава X * и Y * - оптимални решения двойна двойка.

Трето двойственост теорема. Стойностите на променливите ай в оптималното решение на проблема с двойна са оценка на въздействието на свободните термини BI системата от ограничения - неравенства директен проблем върху стойността на целевата функция на този проблем:
δf (х) = BI ил

Решаването метод ZLP симплекс, ние едновременно решаване на двоен ZLP. Стойностите на променливите на двоен проблем у,. в оптималния план, наречен обективно определени, или двойна оценки. В приложни проблеми с двойна оценки ай често се нарича скрити, цени в сянка или прогнозите за значителни ресурси.

Имотът е взаимно двойна проблеми

В един проблем търси максимално линейна функция, а другият - най-малко.
Коефициентите на променливите в линейна функция на една задача са свободни членове на ограничения на системата в друга.
Всяка една от задачите, определени в стандартен формат, в които проблемът за максимизиране на всички неравенства формират ≤. и проблемът за свеждане до минимум на всички видове неравенство ≥.
матрица на коефициентите на променливите в ограниченията на двете системи задачи са транспонирани един до друг:
Броят на неравенството в системните ограничения на проблем съвпада с броя на променливите в различна задача.
Условия за не-негативност на наличните в двете проблеми променливи.

Така, ние имаме оригиналната проблема I и неговото оптимално решение х * = (0, 40, 0, 100) и F (х) = 700.

Прилагането на двойственост теорема, ние получаваме решението на двойния проблем на известното решение на първоначалния проблем.
Ние се намери решение на проблема с двойна II у * = (Y1. Y2. Y3), без да се прибягва до метод симплекс, и с помощта на втория дуалността теоремата и известен оптимално план х *.

Помислете неравенства проблем Аз, чрез заместване на х * в системни ограничения.

Ограничение е удовлетворена от строго неравенство, т.е. ресурсите на първи тип, не е достигнат. Така че това не е ограничен ресурс и неговата оценка в оптимална y1 план = 0.

5 * 40 + 0 + 100 = 300 = 300

директен проблем ограничение е удовлетворена като равенство. Това означава, че 2 минути ресурс се използва изцяло в оптималния план е ограничен и оценка съгласно теоремата на ненулев втората дуалността (y2 ≠ 0)

0 + 0 + 100 = 100 = 100

Четвъртото ограничение в двойна Проблемът е равенство
0,5y1 + y2 + Y3 = 5

От 1, 5, 7 строги неравенства (имат надпис "<" или ">. "), След съответното неравенство Проблем II на чифт конюгат изисква да прилага по отношение на равенството имаме:

т.е. у * = (0, 1, 4) - оптималното решение.

По този начин, по силата на втория двойственост теорема, ние бързо намери оптимално решение Цел II, който се възползва от условието, че равенството е най-малко един от двойка спрегнати различия в ограничения на двойна проблеми.

Между променливите на първоначалния проблем и двойни променливи, има дълбока връзка. А именно, след привеждане на два проблема I и II на каноничен формата на първични и вторични променливи на проблема съответстват една на друга, както следва:

След като се установи тази връзка, може да се види, че с решаването на проблема с симплекс I и се получава от последната симплекс таблица (табл.), Ние всъщност се реши проблема и II.

Пишем на масата, като се има предвид връзката между променливите х и и YJ.

В силата на кореспонденцията и II на y1 двойствеността теорема променливи. v5. U7 се изисква да бъде равна на 0, защото х5. x2. x4> 0 стриктно. 4. променлива Y Y 2 Y 3 у 6. взема стойности от индекс линия 1, 1, 1, 4, съответно, като съответстващите им променливи x1. x6. x3. Х7 = 0, като свободна. Така че, от последния проблем на таблица II, без да се правят каквито и да било изчисления, а дори и като се използват само съответните променливи:

влизане Правила данни

Задайте своите въпроси или да направите предложения или коментари могат да бъдат долната част на страницата в раздела Disqus.
Можете също така да изпратите заявка за помощ при справянето с изследвания на наши доверени партньори (тук или тук).