Цифрова обработка на сигнали
Цифрова обработка на сигнали. Развиване на сигнали
Предмет 13. деконволюция на цифрови сигнали
Ако къщата е красиво, ние разбираме, че тя е построена за домакините, но не и при мишки.
Хризип. Древногръцкият философ. III v.d.n.e.
Деконвулсия подобен на археологията. Предизвикателството - да се възстанови развалините на къщата. Успокояващото ако отломките на земята. Но дори и само на пясъка, а след това да се разбере дали една къща там за хората или за съхранение на мишки, не е толкова лесно.
Григорий Старцев. Урал геофизик. ХХ век.
1. Концепцията за развиване. Определяне деконвулсия. Особености деконвулсия. Стабилността на деконволюция филтри. Работа nedirakoidnyh функции.
2. Обърнете отговор филтър импулс. Изчисляване на обратни филтърни коефициенти. Пример филтър инверсия оператор.
3. Оптимални деконволюция филтри. принцип оптимизация. Пример деконволюция Изчисляване на оптималното филтъра. Уравнението на оптимално инверсия. Левинсън уравнение.
4. Рекурсивно деконвулсия. уравнение рекурсивен деконволюция филтър. Пример рекурсивен деконволюция.
5. Филтър за компресия сигнали. функцията за трансфер на филтъра. оптимални филтърни оператори.
Основната цел на развиване (деконволюция) - вярно възстановяване форма сигнал извършване информацията за изпитване или физически процес, естеството на явлението, и т.н. след нарушаването му по време на регистрацията на линейна система - измерване на пътя инструмент (хардуер или функция на инструмента) или комуникационен канал. Естествено, трябва да се възстанови информацията за характеристиките на изкривяване на системата, на първо място, на импулсната характеристика на системата или на честотата на предавателната функция. За извършване на деконволюция се прилагат филтри, честотните характеристики на които са обратен честотата характерни нарушаване системи. Изграждането на такива филтри не винаги е възможно. Така, не е възможно по принцип да се възстанови честоти на сигнала, които са били напълно потиснати и намаляването на честотните компоненти атенюирани на нивото на шума, като има значително усилване на дисперсията на шума, при който полезният сигнал може да бъде напълно загубен.
Въпреки това, развиване, или обратна намотка се използва за други задачи за обработка на данни. Така че, в геофизика се прилага за компресиране на сигнала, за да се увеличи времето или по пространствена разделителна способност на резултатите от измерването. В магнитен търсене, използвайки деконвулсия преизчислява аномални полета надолу. В ядрените геофизиката методи деконвулсия са в центъра на количественото тълкуване на резултатите от измерванията, подпомогнати от принципа на суперпозиция на области на ядрената физика.
По неизвестни честотни характеристики на изкривяване на системата тя може да бъде сляп деконвулсия (сляп деконвулсия). Blind деконвулсия - много по-сложен проблем, който няма общи решения и съобразени със специфичната априори информация за специфични приложения.
13.1. Концепцията за развиване.
За достатъчно сложен физически представителство в момента (координират) на региона лесно да се разбере деконвулсия в представителството на честота. Да приемем, че системата за запис се провежда абсорбцията резонанс на енергия и на фазовото изместване на хармонични трептения от входния сигнал, състояща се от, например, хармонична грях превръщане 0 т 0.5 грях (0 - / 4). Съответно, за да се възстанови оригиналния операция вълната деконволюция е да се извърши тази амплификация хармоници в изходния сигнал от 2 пъти и извършване на обратно фазова промяна / 4. За едно хармонично изпълнение на такава операция не работи. Но практически деконвулсия проблем е много по-трудно, тъй като изисква, като правило, пълното възстановяване на първоначалния спектър сигнал с постоянен характер.
Определяне деконвулсия. Ако директно намотка цифров сигнал х (к) в импулсната реакция Н (п) на линейната система (филтър) имат формула:
у (к) = Н (п) ③ х (к) H (z) X (Z) = Y (Z), Y (Z) =
проблем деконволюция в обща форма - определяне на сигнала на входа на линейната система за стойностите на изходния сигнал, т.е. Реакционната отстраняване (импулсната реакция) на системата на сигнала и възстановяване на първоначалната форма на сигнала, което е много важно, например за системи за запис:
X (Z) = Y (Z) / H (z) = Y (Z) Н-1 (Z) у (к) ③ ч -1 (п) = х (к), (13.1.1)
където индексът "-1" трансфер функция символично означен обратен оператор филтър Н-1 (Z) = 1 / H (Z), т.е. деконволюция оператор, обратен директно оператор намотка (импулсна система отговор). Съответно, когато Z-трансформация деконволюция оператора на обратен получаване на:
Н-1 (Z) = 1 / H (Z) ч -1 (п). (13.1.2)
Очевидно е, че ако има H (Z) Н-1 (Z) = 1, тогава Z обратна трансформация на този израз, трябва да имаме:
където o (п) - Kronecker импулс. В този последователно намотка на сигнала х (к) с з системен оператор (к) и з деконволюция оператор -1 (к) е еквивалентна на навиване на сигнала х (к) с импулсен Kronecker, че не трябва да променя формата х (т) сигнал.
Когато Z = ехр (-j) Всички по-горе се отнася също и до спектралното представяне на операторите. Един пример на оператора на инверсия чрез спектрален представяне е показано на фиг. 13.1.1 (оригинал HN оператор спектрална плътност H (ω) обратен Н спектрална плътност -1 (ω) обратен оператор ч -1 п в пробите първоначалните интервал).
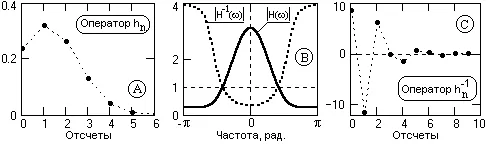
Особености деконвулсия. Уравнение (13.1.2) ви позволява да направим някои изводи за особеностите на извършване деконвулсия.
Когато не ограничен импулсен з отговор (п) обратен оператор ч -1 (п) е по принцип ограничена. Например, ако на импулсната реакция е представена от нормализирана дипол часа (п) = (1 + А) = Н (Z), тогава имаме:
Н-1 (Z) = 1 / (1 + Я) = 1-Я + 2-а 3 Z 2 + Z 3.
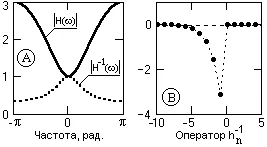
Това е наистина почти никакви намотка оператори, чиито енергия на всички зони с ограничен достъп на основния честотен диапазон, близки до нула. Когато инверсия спектрална функция на операторите в тези области, които имат остри спектрални пикове, които са трансформация обратната Фурие се оставя бавно да се разпада функция оператори. Един пример за това явление е показано на фиг. 13.1.2.
От това следва, че за да се извърши точно деконволюция е необходимо да има безкрайно дълго обратен филтър оператор. На практика, развиване, се извършва, ако операторът на обратна бързо избледнява и да са ограничени. Но използването на съкратени оператори води до известна деконвулсия грешка, стойността на които трябва да се наблюдава.
Имайте предвид също така, че функциите на прехвърляне на системи са склонни да имат нискочестотен характер а. Обръщане на операторите на такива системи е винаги свързани с усилване на високи честоти, което води до висока печалба обратен филтри промяна в шума, което може да доведе до загуба на желания сигнал между амплифицирани колебанията на шума.
В допълнение, бързо затихване на оператора на развиване, е необходимо, но не достатъчно условие за изпълнението на развиване.
Стабилността на деконволюция филтри. Ч функция (Z) в израза (13.1.2) има единични точки - функционални нули, стълбове, които стават функция Н-1 (Z) = 1 / H (Z) и определяне на стабилността на филтъра за обратен. За деконволюция филтър, за да бъде стабилен, редица 1 / H (Z) трябва да се събират, т.е. функционални полюси трябва да бъдат извън единица кръг на Z-равнина (в кръга използване символи Z -1).
Н (Z) полином на ред N може да бъде разложен на основните фактори N - binomials (диполи):
където а, Ь, с, ... - корените на полином. Манипулиране предавателната функция:
Ако всяка от функциите на диполи (13.1.4) е минимално фаза dirakoidom, т.е. диполи корени са извън единица кръг в Z-равнина и нула потребителя дипол модули винаги по следват зад тях първите членове (в този случай: | а |> 1, | б |> 1, | а |> 1), функция H на ( щ) също е минимално фаза dirakoidom. Максималната енергия на импулсната реакция dirakoida минимум фаза се концентрира в първоначалното си част, и се брои номер на последователност се погасява. Функцията 1 / H (Z) ще бъде също предавателната функция на минималната оператор фаза осигурява състояние (13.1.3) и обратен - конвергентна серия стабилен филтър. Например, филтър, който изпълнява функцията за трансфер (13.1.5), в най-общ вид, могат да бъдат направени под формата на филтри, свързани в серия, всеки от които има предавателната функция от следния вид (за първия филтър):
Следователно, както и директно от израза (13.1.5), тя също така следва, че по-голяма стойността на корените на филтърните модули (по-далеч от кръг поле филтър единица), толкова по-бързо се разпада обратен оператор.
Проверява се стабилността на обратен филтър оператор в Mathcad е показано на фиг. 13.1.3. Модули всички корени по-големи от 1, на обратни полином полюсите са извън единица кръг на Z-равнина, операторът на обратен и трябва да бъдат стабилни.
Фигурата показва също оператор деконволюция който е получен чрез обратна трансформация на Фурие на предавателната функция Hi (). Операторът е безкраен, но бързо избледнява, което гарантира висока точност деконвулсия използване на ограничен брой членове на оператора на филтъра (определени от потребителя за дадена точност).
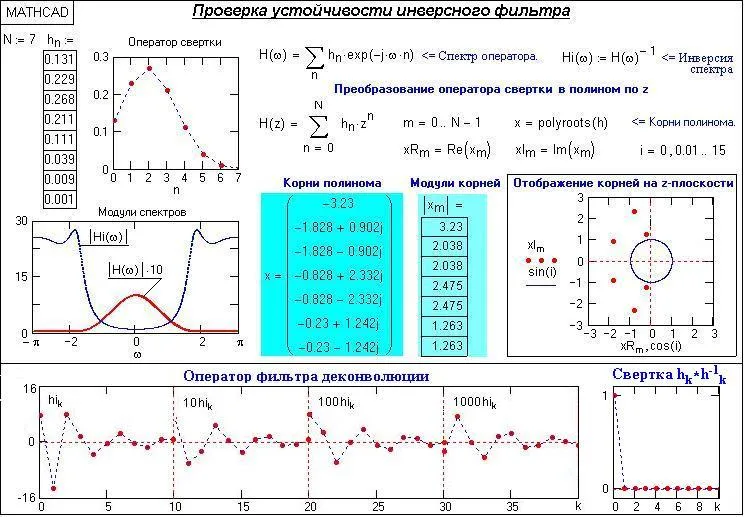
Фиг. 13.1.3. Пример стабилен обратен филтър.
Пример 2: Да се измести горното твърдение с една позиция надясно и да се запази същото енергия операторът ще се h0 = 0,001. Е необходимо да се оцени стабилността на HN обратния намотка оператор =, N = 7.
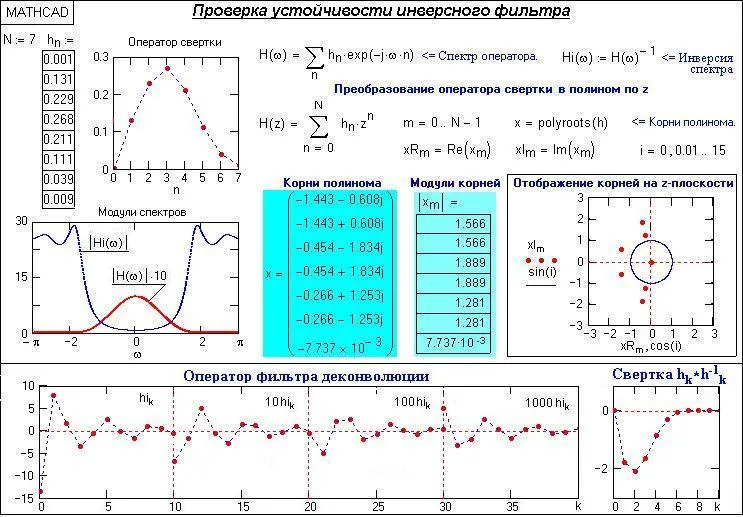
Фиг. 13.1.4. Пример нестабилна обратен филтър
Резултатите от тестването на нови съпротивление деконволюция оператор е показано на фиг. 13.1.4. По подобен начин на операторите намотка модули на спектъра са почти идентични. Но поради фаза промяната на относителната оператор на първия (фиг. 13.1.3), корените на неговата Z-полином претърпели значителни промени, и модула е един от корените на по-малко от 1. Въпреки че операторът изчисленото деконволюция също представлява редица ограничен енергия, но състоянието (13.1.3) не е изпълнено, като се демонстрира чрез навиване резултат HK * ч -1 к.
Работа nedirakoidnyh функции. Ако H (Z) - reversoid, т.е. корени съставни диполи, разположени вътре и на единица кръг в Z-равнина, стабилно циркулация H (Z) е antiimpulsom (с отрицателни сили на Z) и да се използва, е необходимо да има "бъдеще" стойност на входния сигнал.
Ако диполи функция (13.1.4) и представляват dirakoidy и reversoidy, лечението се определя от общото центърът на тежестта и серия Laurent:
т.е. обратен филтър оператор е двустранно и не непременно симетрична, както обикновено по-рано двустранни оператори.
Пример 3. Филтър функцията за трансфер: H (z) = 1-2z. Inverse функция Н-1 (Z) = 1 / (1-2z). спектри честота на функциите, показани на Фиг. 13.1.5.
Поле ZP = 1/2 функция и се съхраняват в единица кръг на Z-равнина.
Препишете експресията за обратна на филтъра, както следва:
Този израз е разширяване серия в правомощията на 1 / г и клони към окръжност с радиус 1/2 Z → . Коефициентите на силите на 1 / Z са съответно коефициентите на филтъра за обратен с координати (N), т.е. филтър работи на "бъдеще" на пробите от входния сигнал (вж. фиг. 13.1.5).