Аксонометрични фигури проекционната равнина - инженерна графика - сайт за информационна сигурност

Изграждане на плоски полигони изображения намалява с прогнозите в строителството аксонометрични на техните върхове, които са свързани помежду си с прави линии. Като пример, помисли за изграждането на петоъгълник е показано на фиг. 1.

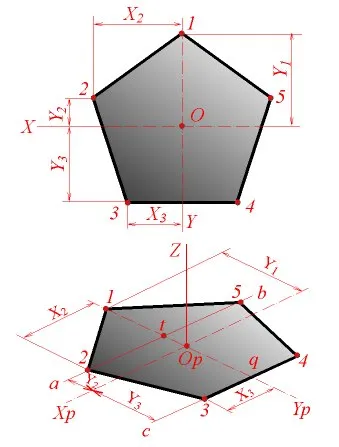
Фиг. 1. Изграждане на петоъгълник.

Линии X, Y, се приема за координатните оси. Равен изометричен ос XR и Yr (фиг. 1). За точки изображения 1 YR оста на достатъчно за отлагане интервал или -1, равни по големина Y1 координира. След това се нанася в една и съща страна на точката на сегмент Или Или -t, равна на координатната Y2. и чрез т изпълнява директно аб, успоредна на оста XR. X2 координати на върховете на петоъгълника 2 и 5 са ​​равни по сила, но на различен знак; Следователно изометричен илюстрация отложи в двете страни на точка Т сегменти т-2 = трет-5 = X2. 3-4 петоъгълник страна успоредна на оста X. Поставянето настрана точка Q ос Yr сегмент р-Or. равно на Y3 координира. изготвили CD, успоредна на оста XR. и съкрати върху него се простира р-3 = р-4 = Х3.

Чрез свързване на точки 1, 2, 3, 4, 5 прави линии, ние получаваме изглед в перспектива на петоъгълник.

Изграждане аксонометрична проекция на крива равнина се редуцира до изграждане на поредица от издатини на своите точки и свързването им в определена последователност. Фиг. 2 илюстрира структура на елипса, разположен в равнината на оси X, Y.

В схема елипсата определи брой точки и тяхното правоъгълна координати X и Y. След аксонометричен ос или отложи точката заедно Р сегменти ос х, равна по размер на координати X целевите точки, и по YR оста - сегменти, равни по размер половина Y координати (показани изграждане на точките а, в, с, D). Чрез краищата на сегментите да се направи директно успоредно XR на оси. Yr; при тяхното пресичане получи аксонометрична проекция на съответните точки, които свързват гладка линия.

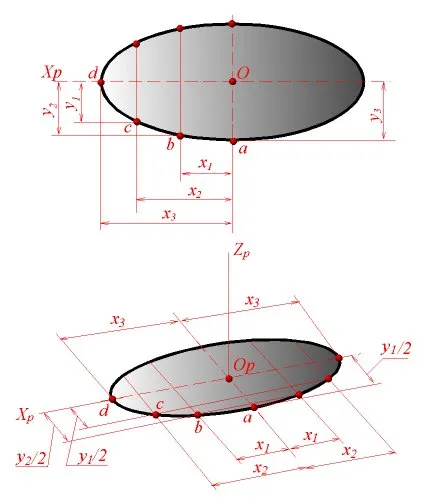
Фиг. 2. Изграждане на елипсата.

строителство триизмерно обиколка

Както е известно, по периферията на правоъгълен издатък, разположен в равнина под ъгъл V (фиг. 3) с равнина Р на издатъците е елипса. Големи Ар BP ос на елипсата - проекцията на диаметър AB на, успоредни на равнината P. Фигура. 3 е очевидно, че интервалът Ар BP е перпендикулярна проекция Cp Np. Dp и малката ос на елипсата Ef (диаметър на издатината DE) на съвпада с линията Cp Np.

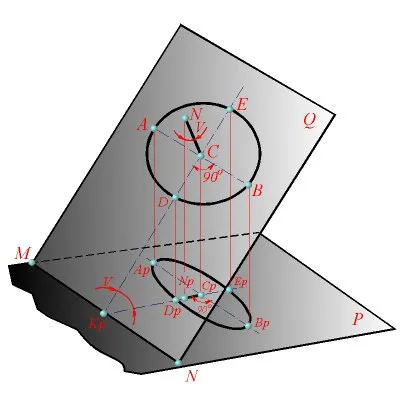
При изграждането на аксонометрични проекции често е необходимо да се изгради образа на кръгове, подредени в координатните равнини, XY, XZ, YZ или в равнини, успоредни на тях. В този случай, нормалните до оста Z, съответно, са плоски кръгове, Y, X. Следователно, посоките на главните оси на елипсите представляващи проекцията на кръговете винаги перпендикулярни оси съответно Zp. Год. X P (фиг. 4), и второстепенни оси съвпадат с посоката на тези оси. Големи-ос съответстват на диаметрите на кръгове изобразени, които са успоредни на равнината на картината. Ако изглед в перспектива на редукцията се извършва в посоките на XR на оси. Год. ZP. главните оси на елипсите 1, 2, 3 (фиг. 4) са равни на диаметъра D на кръговете изобразени. В изометрия малката ос на елипсата равен 0,58d. В dimetric прожекционни второстепенни оси на елипсите 1, 3 (фиг.4) равни г / 3 и малката ос на елипсата е 2 0,88d.

Ако изометрия е построен без намаляване на координатните оси, главните оси на многоточието са 1,22d и второстепенни оси на многоточието са равни на 1,3 0,35d, ос на елипсата е равно на 2 0,95d.

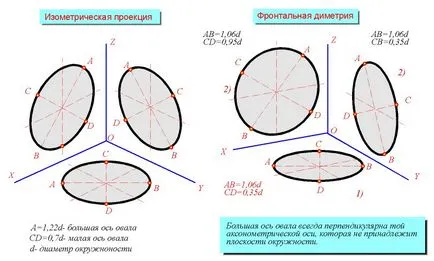
Фиг. 4. многоточието в различни проекции.

С някои умения за съставяне елипса е достатъчно за осем точки - фиг. 5 точки 1 и 2 - краищата на главната ос, 3 и 4 - краищата на малката ос. Точки 5, 6, 7, 8 - аксонометрична проекция завършва диаметри кръг, успоредна на координатните оси X, Y. За да се определи повече точки могат да се прилагат по следния метод. На ръба на лентата от хартия (фиг. 5), за да се отложи сегментите AB и AC, съответно, са равни голям и малък елипса ос. Ако точка С направи плъзгача (Фигура 5.) По голямата ос на елипсата и точка Б - по малката ос, точка А описва елипса.

В някои случаи, на практика допустимите приблизителни проследяване елипси с шублер. Изграждане на изометрична проекция кръг с диаметър D, която е успоредна на равнината на някои от координатната равнина се препоръчва, както е показано на фиг. 5.

Фиг. 5. Изготвяне на елипсата.

Приблизителният диаметър на елипсата проследяване може да се направи в кръг в равнина, успоредна на XZ и обиколката лежат в равнини, успоредни на XY и Zy. Редът на чертеж е показана на фиг. 5.

диаграма умножаване размери на изкривяване коефициенти

Задача умножаване на линейните размери (L) на коефициентите на 1.22, 1.06, и т.н. значително опростена, ако се приложи вместо аритметични изчисления с използване графичен строителство схема (фиг. 6).

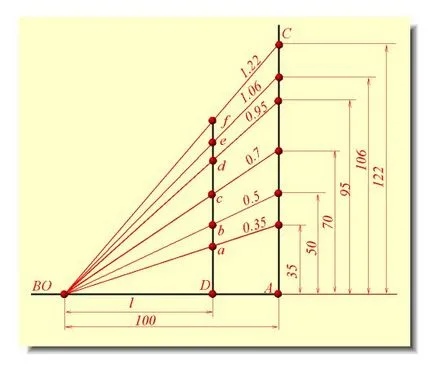
Фиг. 1. iagramma умножаване размери на коефициентите на деформация.

Като две взаимно перпендикулярни прави линии AB и AC, една от тях, като АВ, от точка А поставяне на 100 мм. След това, в AC от една и съща точка на полагане 35, 50, 70, 95, 106, 122 mm. Полученият точка е свързана с точката О.
Ако точка O от хоризонталната разделителна способност отложи л, комбинираните вертикални секции Da, децибела. Df са съответно 0,35 л; 0,5 л;. ; 1,22 л.

На наклонени линии прилага диаграма стойности коефициент, които съответстват на тези линии.

Използване на значително опростена диаграма, ако се извърши на милиметрова хартия.