Вторият знак на екстремни функции
ако и след това - максималната точка.
Както можете да видите, тази функция се изисква наличието на екстремум на функция производна поне до втория ред в точката.
Намери екстремуми на функцията.
Нека започнем с определението на полето:
Разграничаваме оригиналната функция:

Производното става нула, когато х = 1. това означава, че е на мястото на евентуален екстремум. Ние сме втората производна на функцията и изчисляване на стойността му при х = 1.
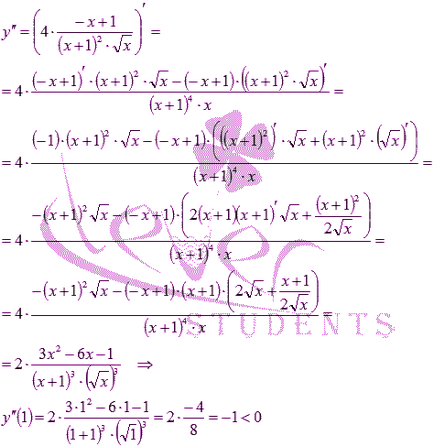
Следователно, съгласно втория достатъчно условие за екстремум, х = 1 - максималната точка. След това - максимална функция.
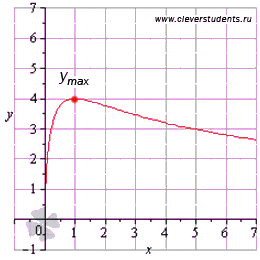
На трето място, достатъчно условие за екстремни функции.
Нека функция у = F (х) има производни на N-ти ред в близост до точката, и производни на N + 1-ия ред на мястото. Да.
ако п - дори и тогава - инфлексна точка;
ако п - странно, а след това - крайна точка, и
ако и след това - на минималната точка;
ако и след това - максималната точка.
Намерете точката на екстремни функции.
Първоначалната функция е цяла рационална, потребителите е целия набор от реални числа.
Производно изчезва при следователно възможно точка екстремум. Ние използваме трета достатъчно екстремум.
Ние сме втората производно и се изчислява стойността си в точките на възможно екстремум (междинни изчисления пропуснати):

Следователно, - максималната точка (за достатъчен критерий третата екстремум има и п = 1).
За да се изясни същността на третата производна намерите точки и изчисли стойността му в тези пунктове:

Следователно, - на инфлексна точка на функцията (п = 2 ф).
Остава да се справят с най-важното. Ние считаме, четвърти производно и се изчислява стойността му в този момент:

Следователно, - минимална точка на функцията.

- висока точка - минималния точка на функцията.
10. Определяне на крайности функционалните
Функцията у = F (X) се нарича увеличаване (намаляване) на определен интервал, ако x1
Ако диференцируема функция на у = е (х) в интервала [а, Ь] увеличава (намалява), тогава F '(х) производно в този интервал 0
Хо точка се нарича локален максимум (минимум) на F на функция (х), ако съществува квартал на Хо. за всички точки, където неравенството е (х) ≤ F (Ho) (е (х) ≥ е (Ho)).
Точка максимални и минимални точки се наричат крайни. и стойностите на функцията в тези пунктове - неговите крайности.
екстремалната точка
Необходими условия за екстремум. Ако Хо е точка екстремум на F функция (х), след това или F '(Ho) = 0, или е (Ho) не съществува. Тези точки се наричат критични и функцията се определя в критичната точка. Излага на функции, за да бъдат намерени сред своите критични точки.
Първото условие е достатъчно. Нека Хо - критична точка. Ако F '(х) при преминаване през точката Хо променя знак плюс минус, след това при точката функция Хо има максимален, в противен случай - поне. Ако минаваща през критичната точка на деривата не променя знак, а след това на мястото, Ho не екстремум.
Вторият достатъчно условие. Да предположим, че F функция (х) е производно F '(х) в съседство на Хо и втората производна на мястото Хо. Ако е "(Ho) = 0,> 0 (<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На интервала [а, Ь] функцията Y = е (х) може да достигне до най-малкия или най-голямата стойност или критичните точки или сегменти в краищата [а, Ь].
Пример 3.22. Виж екстремум на F функция (х) = 2 х 3 - 15x 2 + 36x - 14.
Решение. Тъй като е '(х) = 6x 2 - 30x 36 = 6 (х -2) (х - 3), критичните точки на две и Х1 = Х2 = 3. екстремумите може да бъде само в тези точки. Така че, докато се движите през точка x1 на = 2 деривативни промени подписват от плюс до минус, а след това в този момент функцията има максимална. При преминаване през точка х2 = 3 деривати промени знак минус до плюс, така че в точка х2 = 3 за функцията най-малко. Изчисляване на стойности на функцията в точки Х1 = Х2 = 2 и 3, ние откриваме екстремумите на функцията: максимум е (2) = 14 и минималната F (3) = 13.