Урок - преобразуване продукти от тригонометрични функции в размер на

Кратко описание на документа:

Въпреки факта, че тригонометрията, наука, имаше доста дълго време, тя не е загубила своето значение и днес. В различните науки има проблеми, чието решаване на студентите трябва да се занимават с тази област. Поради тази причина те трябва да могат да се справят с примери с различна сложност, помислете за функцията, съдържащ задължително, косинус, тангенс и котангенс и т.н.

Тъй като тригонометрията съдържа огромен брой формули, без които опростяване на израз ще отнеме много време. Ето защо е много важно е да си спомняш и разбиране на тези формули. Ако разбирате процеса за отстраняването им, лесно можете да си ги спомня и се прилагат на практика. За тях, за да остане в паметта за дълго време, трябва да бъдат засилени в практиката. Ето защо, учителите трябва да се обърнете към къщата на голям брой тригонометрични изрази и уравнения за ученици.

Децата в училище вече знаят как е необходимо да конвертирате сумата от тригонометрични уравнения в продукта. Как може да изпълнява обратен процес, ако е необходимо? Понякога за опростяване на израз, че ще бъде необходимост.

Тя започва с разглеждане към него. Писмени творби на някои TNA задължително косинус на една и съща стойност. Трансформира този израз от една малка част, където числителят е сумата от задължително виждаме сумата и разликата от аргументите, разделена на две.

По същия начин, продуктът се превръща в синусов някои е синуса на тон.

С цел да се осигури изразяване данни практика предложената за решаване на някои примери. Първият от тях е предложено да намерите числен отговор за изразяване, която е продукт на синуса и косинуса 2x 9x. При решаването на този пример се използва предварително проучен формула. Екранът извежда подробен пример на решението също така показва какво се използва нещо като формула.

Третият пример предлага бег експресия, която се състои от продукта от три синус известна степен стойности. В опростяване формула се използва в продукта превръщане на задължително сума. В решаването на този пример подчертава факта, че функцията косинус е дори функция. По този начин, знаците са определени правилно. Изходна отговор. Обемът на разтвора са достатъчни, но ако се стъпка по стъпка, за да го разгледа, след това нищо няма да остане неизвестен.

Както вече споменахме, с помощта на тази презентация може да се направи интересен урок за десятък. Изтегляне на материала може да обучава и студенти. С него можете визуално да покаже стъпка по стъпка студент разтвор на примери, в които сходството на студентите ще се намира, както по време на домашното и самоконтрол и работата в училище.

Преобразуване работи в размер на тригонометрични изрази

Вече знаете, че който и да е математическа формула, използвана в практиката от дясно на ляво и от ляво на дясно. Следователно прилагане на формулата на заден ход, ние можем да работим тригонометрични функции, за да се превърнат в пари.

Преминаване от формула суми Sines и ТЕ аргументи ЕО в proizvedeniesin (а ​​+ T) + грях (S - т) = 2 греховете струват

можете да получите друга формула:

грехове струват = (продукт на задължително аргумент ес косинус аргумент ТЕ е равно на половината от сумата на задължително сумата от ES аргументите и ТЕ задължително и разликата Ес аргументите и Te, и разликата се приемат като тази на аргумента, стои под знака на задължително изважда ъгъл стои за знака на косинус. )

По същия начин, с формула възлиза косинус трансформира аргумент и ТЕ ЕО в COS продукта (ите + T) + COS (и - т) = 2 КМБПЗК разходи получи

КМБПЗК цена = (продукта Ес на косинус аргумент и ТЕ е равно на половината от сумата на тези аргументи косинус на косинус и тяхната разлика).

И от разликата косинус преобразуване формули ЕО и ТЕ аргументи proizvedeniecos (а + т) - COS (S - т) = - 2sins Sint имат

грехове Sint = (продукт на Синиш и аргументи ове ТЕ половин косинус е равен на разликата на тези косинус аргументи и техните количества).

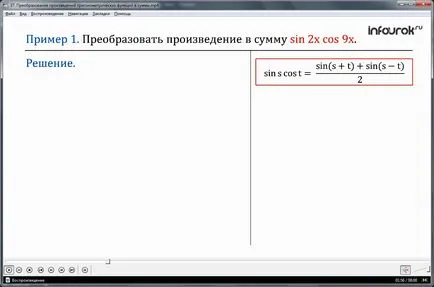
Пример 1. Продуктът се превръща до cos9h сумата sin2h.

Решение. Когато решението ще бъде да се използва формулата грехове струват =. където а = 2, т = 9х. Тогава можем да запишем

sin2hcos 9х = (при положение, че

грях (у) = -sinu получаване) = (половината задължително единадесет X и синусите седем X).

Отговор: sin2h cos9h =.

ПРИМЕР 2: Продуктът от сумата от COS (2х - Y) COS (х + 4Y) (продукт на косинуса на аргумента, двата X минус ш на косинуса на аргумент X плюс четири Y).

Решение. Когато решението ще бъде да се използва = на разходите формула КМБПЗК. където S = (2-г), т = (х + 4Y). след това

COS (2х - Y) COS (х + 4Y) = = = разкриват скоби. ние извършване на изчисления и да получи

= (Половината от сумата на косинуса на аргумента, три плюс три X Y и косинус на аргумент X минус пет Y).

ПРИМЕР 3 Опростена експресия sin20 ° sin40 ° sin80 °.

Решение. Ние прилагаме формулата: греховете Sint =.

грях 20 ° грях 40 ° грях 80 ° = ∙ грях 80 ° = ∙ грях 80 ° =

(Трябва да отбележим, че косинус - функцията е дори, а след това

= ∙ грях 80 ° От cos60 ° =

= ∙ грях 80 ° = ∙) ∙ грях 80 ° =

(Забележете, че грях 80 ° = грях (90 ° - 10 °) = cos10 °, следователно получаване на това)

= ∙) ∙ cos10 ° = разкрие скоби = ∙ cos10 ° - ∙ cos10 °

(Приложимо формула КМБПЗК разходи =)

Отговор: sin20 ° sin40 ° sin80 ° =.

Пример 4. решаване на уравнение 2 sin2h cos9h - sin11h = 0.

Ние се трансформира в лявата част на уравнението с помощта на формулата

грях и COS Т =. gdes = 2x, Т = 9х получи

2 ∙ - = sin11h sin11h =.

Така че, това уравнение е еквивалентно на уравнението = 0 (минус задължително седем X е нула). Така че, = πn, където х =.