уравнение г
Уравнение на Бернули
Daniila Bernulli уравнение е основната уравнение на хидродинамиката. По-долу това уравнение подкован за стабилно движение гладко различна течност се решават с помощта на които основните проблеми на хидродинамиката. Ние въведе концепцията на специфичната енергия на елементарните потоци и течен поток.

Мас течност заема определен обем V, която е под налягане, равно на енергията на налягането r.Potentsialnaya rV.Udelnaya същото potentsialnayaenergiya energiipV налягане, равно на потенциала разделен от силата tyazhestidannogo obemagV, т. Е.
Пълен доставка на специфичната маса на енергия на течността е равна на сумата им, R. Ф. и предвид изразите (а) и (б), ние можем да напишете
Освен това, течната маса м движи със скорост и има кинетична енергия; но тежестта на тази маса е равна на мг, и специфичната кинетичната енергия на струи равен
Добавянето на експресия (в) и (г), ние получаваме израз пълни udelnoyenergii елементарни потоци
Ето - специфична кинетична енергия;
- специфична енергия налягане и позиция.
Общият специфична енергия поток E izudelnoy сумата от потенциалната енергия и специфичната кинетичната енергия Ekpotoka.
За случая с гладко промяна на постоянен поток течност специфична потенциална енергия на всички места за ефективното сечение е един и същ и равен
Fluid поток се разглежда като набор от п елементарни потоци, всеки от които има специфична кинетична енергия. Тази стойност е различна за различните потоци, които са поток.
Ние дефинираме средната стойност на това количество в раздела на потока. За да направите това, действителната скорост на елементарни потоци U1. u2. ООН замени средната скорост на потока V; Тогава средната стойност на специфичната кинетичната енергия на потока в този раздел, се равнява на
Тук, - коефициент на Кориолис, отразяващ неравномерността на разпределението на скоростта по напречното сечение на потока (регулиране или кинетична енергия).
Безразмерна фактор е съотношението на действителния поток кинетичната енергия на кинетичната енергия изчислява от средната скорост. Ако профила на скорост в напречното сечение на потока е почти правоъгълна, т.е. Скорост на различни места близки до средните, а след това с коефициент Кориолис близо до единство. Ако скоростта в напречното сечение значително се различават една от друга, а след това с коефициент е много по-голямо от единица.
Да разгледаме например дълбочина поток з = 6 т, в напречното сечение на който скорости са разпределени на триъгълника, т.е. в долната част на скоростта е нула и се издига до повърхността в съответствие със закона за насочване на голямата стойност ipov = 3 м / сек. Средната скорост V В = 1,5 м / сек, и съответната кинетичната енергия
Ние очакваме, кинетичната енергия на потока точно. За тази цел ние се вземат три точки на височина h1 = 1 метър; h2 = 3 m и h3 = 5m, които се намират в центъра слоеве с еднаква височина 2 м всеки. Скоростта на тези точки, съответно u1 = 0,5; u2 U3 = 1.5 и = 2,5 м / сек. Кинетичната енергия на тези три скорости
който е по-висок от средния темп.
Кориолис коефициент получава
.
Въз основа на обработката на множество данни, събрани в реки и канали, се установи, че за големи открити потоци. В равномерно движение в тръби и канали практика.
В бъдеще, освен ако изрично е посочено друго, трябва да се вземат, за да се опростят изчисленията. Въпреки това, трябва да се забравя, че в някои случаи не-равномерно разпределение на скоростта може да бъде стойност значително по-голямо от 1 (два или повече).

Добавянето на конкретна и специфична кинетична потенциална енергия на потока, ние получаваме формулата общата специфична енергия на потока
,
и това, експресията на (Е) и (G), имаме
, (72)
т.е. общата плътност специфична енергия на потока, равна на сумата от кинетичната и потенциална специфични (налягане и позиция) на потока енергия. Спомнете си, че всички констатации, направени за стабилно, постепенно се променя движението на течността.
Уравнение на Бернули за елементарни потоци. Изберете в реално постоянен поток от течна елементарна струйка (фиг. 21) и определяне на специфичната енергия на течността в две произволни части 1-1 и 2-2. Височина позиции на центровете на първата и втората секции са съответно Z1 и Z2; хидродинамично налягане и същи точки P1 и P2 поток курс - u1 и u2. След това, общата енергийна плътност от елементарни потоци в секцията 1-1 въз основа на формула (71) е равно на
Почти винаги, тъй като част от общата енергия, изразходвана за преодоляване съпротивителната сила (триене), когато течността се движи от раздел 1-1 на раздел 2-2. Ще означаваме тези загуби. След това, в съответствие със закона за запазване на енергията може да пише, че и като се има предвид изразите (ж) и (з), получаваме
. (73)
Уравнение (73) и има Бернули уравнение за елементарните потоци на реално течност по време на стабилно движение, което създава връзката между скоростта на движение, налягането в течността и позицията на точка в пространството. Това е валидно за всеки две секции, така че да раздели 1-1 и 2-2 са взети произволно. Уравнение (73) и може да бъде представен графично (фиг. 21). Ако се комбинират течни нива в пиезометри прикрепени към множество секции, ние получаваме линия р-р, който се нарича пиезометричната линия и показва изменението на специфичен потенциалната енергия по дължината на елементарните потоци. Ако се свържете точките, които във всяка сечение вертикална изобразяват общата специфична енергия (и такива условия наистина могат да получат, както см. По-долу), ние получаваме една линия N-N. Той призова napornoyliniey или електропровод; тя показва промяната в общата енергийна плътност по дължината на потоци. След това е вертикалното разстояние между напречното сечение по какъвто и хоризонтална равнина I -I. съответстващ на началния състав на специфична енергия в първата част, и линията на налягане N-N дава стойността на енергийните загуби ТВ да преодолеят силите на съпротивление на участъка от първата част на този раздел, и разстоянието между налягането и пиезометричната линии - специфичен кинетичната енергия в дадена точка u2 / 2g.
За идеално течност, където не силите на триене в уравнение (IV.7) ТВ = 0 и Бернули уравнение става
Но тъй като тази точка 1-1 и 2-2 са взети на случаен принцип, в общата форма на уравнението на Бернули за елементарните потоци на перфектен течност е написана, както следва:
Уравнение на Бернули поток. Помислете поток при стабилно и плавно се променя движение (фиг. 22). Ние произволно изберете две секции 1-1 и 2-2. осите на които съответно имат Z1 и Z2 - вертикалната координата ос на потока над произволно сравнение равнина о-о, Р1 и Р2 хидродинамично налягане при същите точки V1 и V2 - средна скорост в участъците 1-1 и 2-2.
Общият брой на специфична енергия поток, определен от формула (72): напречното сечение 1-1
,
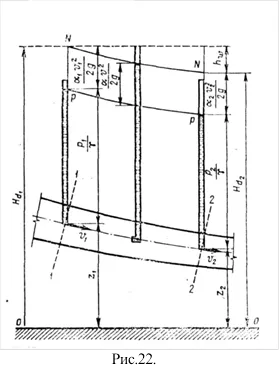
Очевидно е, че тъй като част от енергията, за да се изразходват за преодоляване съпротивителната сила (триене). Означаваме загуба на енергия в тази област -. Тогава можем да запишем, че и заместване на стойностите, получаваме
Уравнение (74) се нарича Бернули уравнението за основния и potokazhidkosti уравнението хидродинамика; Получихме със себе си много формули и решаване на редица практически проблеми. Бернули уравнение установява математически връзка между основните елементи на движението на течност, т.е.. E. средната скорост и хидродинамично налягане.