Униформа и не са единни за движение на тялото по периферията

Специален случай на криволинейно движение - с кръгови движения. Кръгово движение, дори и равномерно, винаги има движение ускорено: скоростта на модул цялото време, насочена към допирателна към пътя, постоянно променяща се посока, така че векторът на ускорение при кръгово движение към центъра на кръга и перпендикулярна на вектора на скоростта.

Обиколка - плоска форма, така че движението в периферната движението е плоска.

Uniform кръгово движение - движение, при което тялото за всички редовни интервали описват една и съща дъга.

положението на тялото на окръжността, определена от радиус вектор $ \ overrightarrow = R $, съставен от центъра на кръга. радиус, равен на радиуса вектор единица кръга: $ \ лява | \ overrightarrow \ дясна | = R $.

Фигура 1. Скоростта на движение и преместване по протежение на обиколката

По време на ATi, тяло, движещо се от точка А до точка Б, прави преместването на $ \ триъгълник R $, равна на акорд AB и минава пътеката, равна на дължината на дъгата л. вектор радиус върти $$$$. Ъгълът изразена в радиани.

Скоростта на $ \ $ overrightarrow движение на тялото в кръг, допирателна към траекторията. Тя се нарича линейна скорост. Модул линейна скорост, равна на съотношението на дължината L на дължината на дъгата от време $ \ триъгълник т $, за която се предава на дъгата: $ о = \ Frac $

Скаларни физическа величина е числено равно на ъгъла на въртене съотношение на радиус вектора на продължителността на времето, през което се случва тази промяна, тя се нарича средна ъглова скорост: $ \ омега = \ Frac $. Единицата за ъглова скорост SI е радиани в секунда.

В равномерно движение на периферна ъглова скорост и линейна скорост модул --- постоянна стойност: $ = конст $; $ V = конст $.

позиция на тялото може да се определи, ако е известно модул радиус вектор $ \ overrightarrow $ и $$ ъгъл, което го прави с оста Ox $ $ (ъглова ос). Ако първоначалните време $ t_0 = 0 $ е ъгловата координира $ \ varphi $ 0, и при време Т е равно на $ \ varphi $, ъгълът на въртене $ Δ $$ \ varphi $ радиус вектор време $ АТ = т -t_0 $ равнява на $ Δ $$ \ varphi $ = $ \ varphi $$ \ varphi $ 0. След последната формула може да получи правото на еднакво движение на точка от кръга:

$ \ Varphi = \ varphi_0 + \ омега т $

Тя ви позволява да се определи позицията на тялото по всяко време $ т $.

Като се има предвид, че $ \ триъгълник \ varphi = \ Frac $, ние получаваме формула връзка между линейните и ъгловата скорост: $ \ омега = \ Frac = \ Frac $

Когато се движи в кръг, както във всяка криволинейна движение, ускорението може да се изрази като сума от нормалната $ _n $ и $ _ $ тангенциални компоненти: $ \ overrightarrow = _ + _ п $

С еднакво кръгъл линейно движение скорост е постоянна и тангенциален компонент на ускорението _ $> = 0 $. Ето защо, в този случай $ \ overrightarrow = _n $.

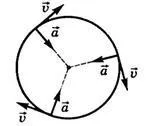
Фигура 2. ускорение и скоростта на движение на еднакво периферен

Ускорение еднакво кръгово движение

В допълнение центростремителна ускорение, равномерно движение на най-важните характеристики са периферно период от време и честота на лечението.

Тираж период $ T = \ Фрак = \ Фрак $ - това е времето, през което организмът произвежда една революция.

конверсия $ процент \ \ \ ню = \ Фрак $ --- е стойност, която е числено равна на броя на оборотите, направени за единица време. Измерено честота 1 / сек.

Период и честота - стойността на реципрочна: $ \ ню = \ Фрак $

При постоянна честота на въртене центростремителна ускорение е пряко пропорционална на разстоянието от движеща се частица до центъра на въртене.

Неравномерното кръгово движение е различен от еднаквите само с това, че тангенциален компонент на $ ускорение _> \ NE 0 $, и линейна скорост V (Т) и ъгловата скорост $$ (т) са нестабилни и са функции от време.

В случай на еднакво ускорено движение по окръжност

Ъгловите координатите за движение по окръжност с ъглова скорост $ \ омега \ наляво (т \ дясно) = \ $ Frac и ъгловото ускорение $ \ varepsilon = \ Frac = \ Frac $, получава право равномерно ускорено движение по протежение на обиколката: $ \ varphi \ наляво (т \ дясно) = _ 0+ \ омега \ наляво (т \ дясно) т + \ varepsilon \ Frac $. където $ \ омега \ наляво (т \ дясно) = \ Frac ;; \ \ \ \ \ varepsilon = \ Frac> $.