Свойства на фазови траектории

1. Решенията и дефинират по същия път. С други думи, решенията за смяна на времето не променя траекторията фаза на системата (1).

2. две или фаза траектории са несвързани или еднакви, т.е. траекторията фаза не може да се пресичат, и два различни траектории фаза не може да се пресичат.

3. Дори ако решението за увеличаване на т произволно близо до точката на почивка. точка на изображението не може да се стигне до момент в определено време.

4. Ако - периодично разтвор на (1), то съответства на затворена фаза траектория. (Без самостоятелно кръстовища).

5. Всяка фаза път е или

а) незатворен линия без самостоятелно кръстовища;

б) затворена крива без самостоятелно кръстовища;

Най-важният въпрос в изследването на динамичните системи е да се идентифицират и да се проучи стационарни (равновесно състояние) движение.

Имайте предвид, че терминът движение за решаването на системата от уравнения (1) е получен от механиката и широко.

а) най-важният вид на стационарни движения - състояние на равновесие, което се определя от крайния системата от уравнения, получени от системата (1), когато производното е нула.

Системата от уравнения (7) има брой м решения.

Следователно, системата (1) има решение.

Ще подчертая, че връзката (9) се отнася и за т промени от нула до безкрайност. Обърнете внимание на някои терминологични трудности, решението (9) се нарича стационарни движения, въпреки че тя съответства на точката пътя към, което е, разбира се, остава неподвижна.

б) Вторият важен клас от неподвижна движение в динамична система са периодично движение, т.е. такова движение, по време на който променливите на състоянието осцилира с период T:

Както бе споменато по траектория, съответстваща периодично движение е затворена крива в пространството фаза.

Необходимо е да се прави разлика между две коренно различни видове периодични движения. Това ограничение цикли и консервативното движение.

Limit цикъл е изолиран затворен път. В достатъчно малък квартал на този път, няма друг затворени траектории. Всички траектории в квартала или "раната" на ограничение цикъл, или извадени от него. (Подробности за този въпрос ще бъде обяснено по-късно)

Много важен феномен в областта - самостоятелно трептене. Самостоятелно трептения съответстват на фаза пространство на стабилен (концепцията за устойчивост ще бъде обяснено по-късно) гранични цикли.

Консервативната движение в техническите системи се срещат много рядко.

в) Третият тип стационарни квази-периодична движения са движения. Те се наричат ​​непериодични движенията, ограничени. Този вид постоянни движения е много рядко в техническите системи.

· Нека се обърнем към въпроса за изучаване на свойствата на стационарни решения.

Стабилността на положението на равновесие.

Ние въведе понятието равновесие позиция Lyapunov стабилност. Първо се опише идеята, а след това ние даваме в изявлението.

Позицията на равновесие се нарича Ляпунов стабилен, ако отговаря на следните условия. Нека първоначалните условия на разтвори на системата (1) е достатъчно близо до позицията на равновесие. В този случай, решението на системата ще остане близо до равновесната точка за всички т> 0.

езика # 949 - # 948; той е формулиран, както следва.

Да - равновесното положение.

равновесното състояние се нарича Ляпунов стабилен, ако за всеки един (произволно малка) положително число # 949; Можете да намерите положително число # 948 (# 949), че ако неравенството:

за целия безкраен интервал от време на неравенството:

равновесното състояние се нарича асимпотично Ляпунов стабилен, ако в допълнение към отношенията (11), (12) държи на условието:

Ако е налице # 949;, че най-малко в един случай не може да намери редица # 948 (# 949), така че когато неравенството (11) неравенството (12) за всички т> 0 тогава положението на равновесие "и" казва, че е нестабилен в смисъл Lyapunov.

Ние наблягаме важно обстоятелство. Стабилността на равновесното положение на системата по никакъв начин не трябва да се резистентност към баланса на други разпоредби. Например, да предположим, положението на равновесие на системата (1) ще бъде. Възможно е, че тя е стабилна и не е стабилен. Или не е стабилен и устойчив.

Илюстрират смисъла на дефиницията за стабилност съгласно Lyapunov на равновесното положение.

пространство фаза е едномерен - права линия. Точката на равновесие х = 0 е асимптотично стабилна, тъй като, за всяка стойност x0 функция х (т) клони към нула с увеличаване на тон.

Решение. равновесие точка е нестабилна, тъй като за всяка функция стойност x0 се отстранява от х = 0.

Тази система отговаря на уравнението на консервативната грижи:

Неговото решение. където А и В # 958; - константи интеграция. пространство фаза е двумерен - равнина.

Под него ще се покаже, че в този проблем всички държавни траектории са вложени безкрайно семейство от кръгове, центрирани при произхода.

Винаги има предвид # 949; можете да изберете # 948; така че кръгът трябваше радиус от по-малко от # 949;. Равновесието позиции x1 = 0, Х2 = 0 Lyapunov стабилна, но не асимптотично стабилна.

· Устойчивост периодични движения.

Определяне на Ляпунов концепция за стабилност за следващите периодични движения. Да предположим, че е периодичен разтвор на (1). Периодично разтвор наречен Lyapunov стабилен, ако за всяка предварително определено положително число # 949; Можете да намерите положително число # 948 (# 949), поради неравенството

От това следва, че за всички т> t0 неравенството

Ако, освен това, при условие

Периодичното движение е асимптотично стабилен в смисъл Ляпунов.

Концепцията за стабилност чрез Ляпунов на равновесното положение много често се използва в областта на науката и технологиите. С периодично движение на ситуацията е по-сложна. В този случай, ограниченията, наложени от условията на стабилност Ляпунов са твърде сурови и рядко изпълнявани. Поради това, той използва по-слаба състояние стабилност нарича орбитална устойчивост на периодични движения.

Периодично движение се нарича орбитално стабилен, ако за всяко # 949; можем да намерим # 948, (# 949) така, че всяка фаза траектория, която, когато т = t0 съхранява в # 948; -neighborhood траектория на периодичния движението, няма да работи за всички т от t0 до безкрайност на # 949; -neighborhood траектория на периодичния движение.

Периодичният движение се нарича орбитално асимптотично стабилен, ако всички споменатата траектория на т → ∞ асимптотично подход траекторията на периодично движение.

Ние обясни концепцията на квартала за траекторията. За това ние се обръщаме към фигура 1, там е показана част от затворен път.

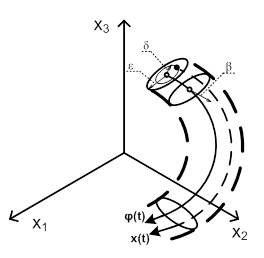
под # 949; - или # 948; -neighborhood път означава извита цилиндър, който е конструиран както следва. Траекторията ще се счита за тънка жица. Вземете една окръжност с радиус # 949; или # 948; с дупка в центъра. Този кръг се поставя по пътя, така че да минава през центъра на кръга. Тогава, кръгът се движи по пътя. В хода на своята гама движение трябва да е перпендикулярна на равнината, допирателна към траекторията. Повърхността, която привлича в пространството на окръжност, извитата граница е цилиндър или "поничка". Припомняме ви, че пътят е затворен.

Orbital стабилност изисква близост не представителни точки разтвори и близо към него при Т = t0 разтвори (Т), и близостта на пътя на точки в пространството, което, разбира се, значително по-слаба състояние. От известно стабилност трябва да Lyapunov стабилност на орбитата на периодичната движение, а не обратното. От орбитална устойчивост не трябва Ляпунов стабилност на периодичния движение.

· Методи за определяне стабилността на положението на равновесие.

Първият метод: определяне на стабилност на положението на равновесие на уравнението на първо приближение. Това уравнение, след приетата традиция в тази област ще бъде наречен линеализираният уравнението.

Вторият метод (често наричани директен метод на Lyapunov) намалява с изграждането на някои функции, които се наричат ​​Ляпунов функции.

1) Критерии за оценка на стабилността в малък равновесие позицията на линеаризиран система (1).

Задачата на изследване на стабилността на положението на равновесие на системата (1) е възможно, с помощта на промяна на променливите, намаляване на проблема за стабилността на положението на равновесие в основата.

Следователно, първоначалната система

превръща в

Системата (20) има положение на равновесие. и системата (21), - произход.

Както е обичайно в литературата, ние замени в писмото, получена от системата Z с буквата х и капка звездата на функцията. тоест, пишем системата на диференциални уравнения, официално същата форма като (20), въпреки че по същество буквата F в оригинал и на новите системи с различни функции са отбелязани. (Модифицирана зависи). Преразпределяне описано по-горе променливи, ако се държи в паметта, няма да доведе до грешки.