Съобщение интеграция с диференциация
Помислете за определен интеграл, чиято долна граница е постоянна и горната променило.
Даване на горната граница на различните стойности, ще получат различни стойности на интеграл; Следователно, в тези условия интеграл на функция на горната гранична стойност
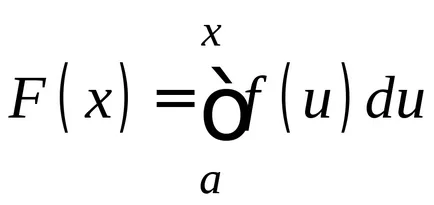
тук

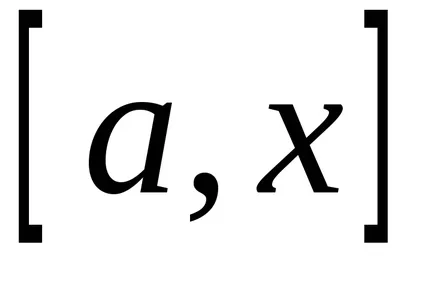
Теорема 1.Proizvodnaya на интеграл от неговата горна граница е равна на подинтегрален
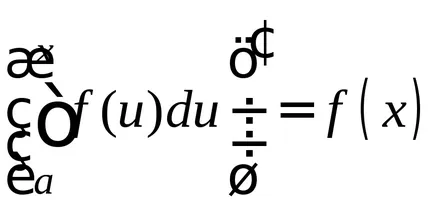
Помислете непрекъснато получаване неотрицателна стойност в интервала
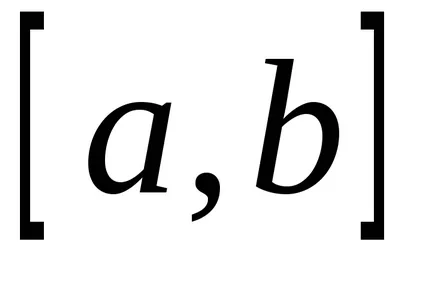
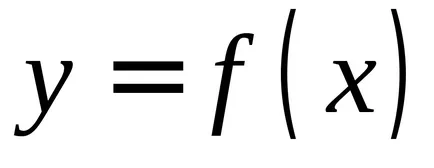

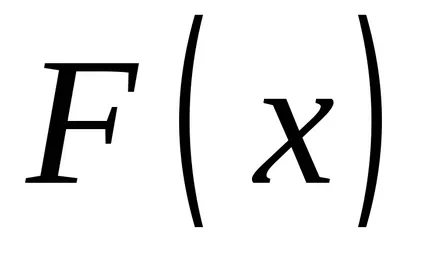
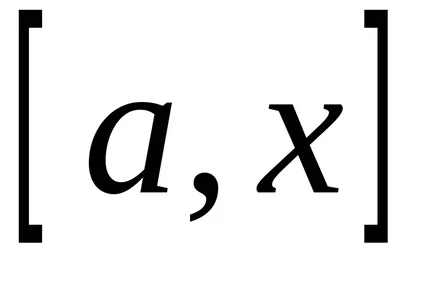
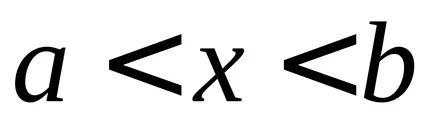
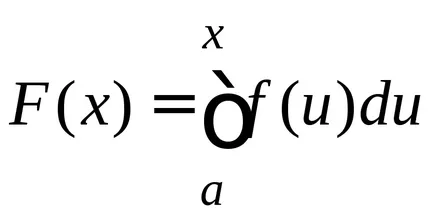
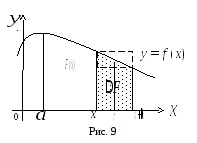
Ако променливата
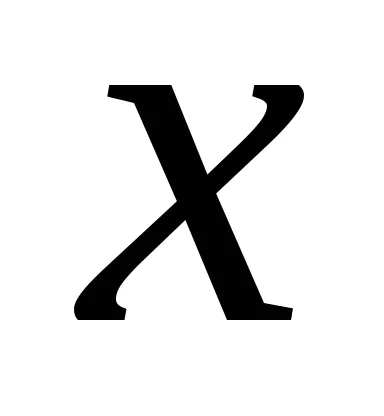

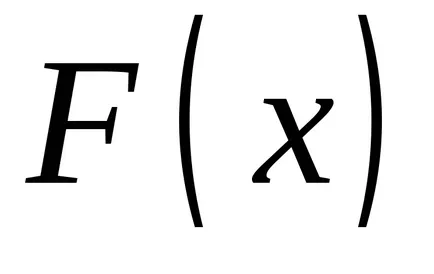

,
където
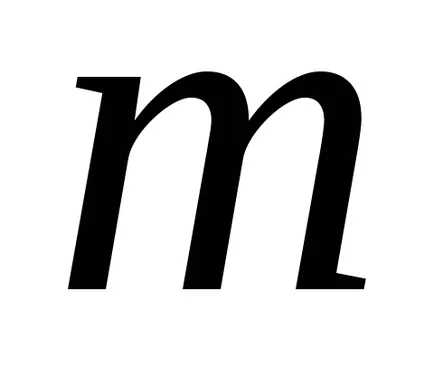
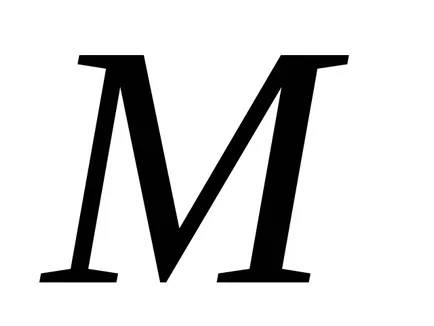
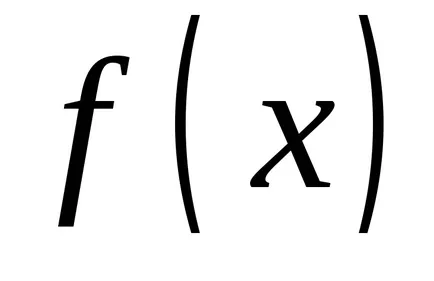
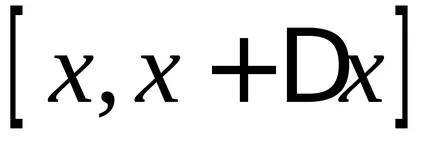


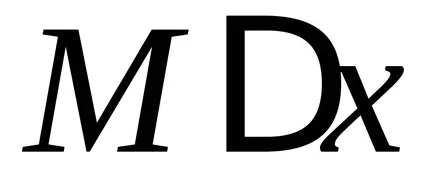

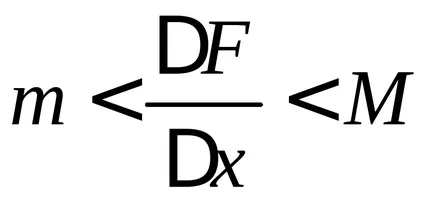
защото
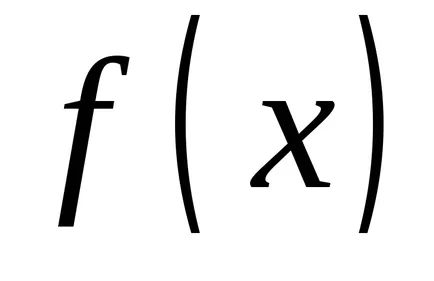
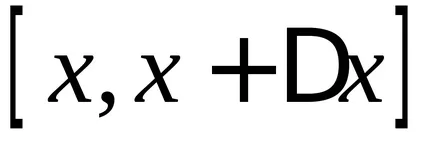
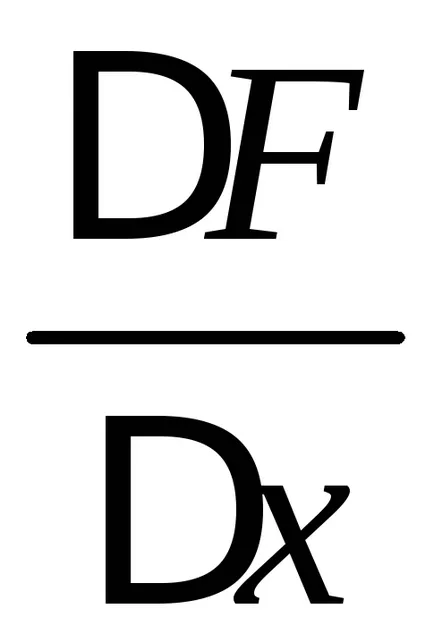
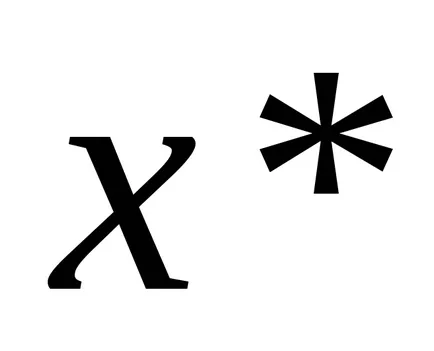
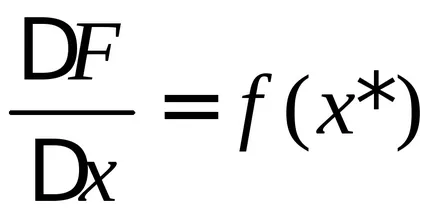
Помислете за граница на този израз с уговорката, че


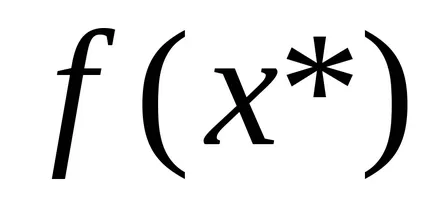
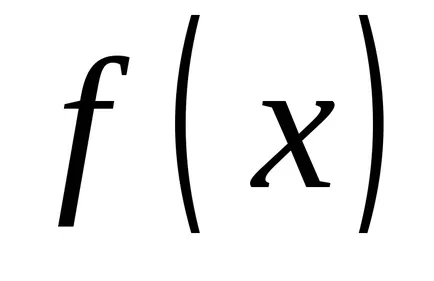
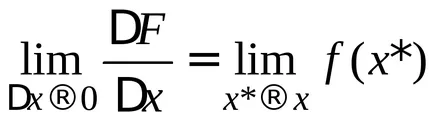
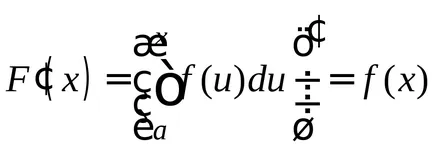
ЗАБЕЛЕЖКА: Тази теорема показва, че интеграцията и диференциация - обратните операции.
В Неопределен интеграл
OPREDELENIE.FunktsiyuF (X), което е производно на функцията подинтегрален се нарича примитивна.
Как да се намери производната е една от основните задачи на диференциала смятане, така че намирането на примитивен тя е една от основните цели на интегралното смятане.
Помислете например за функцията
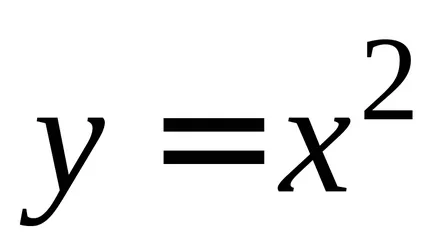
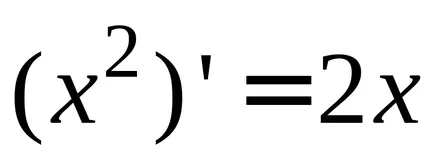
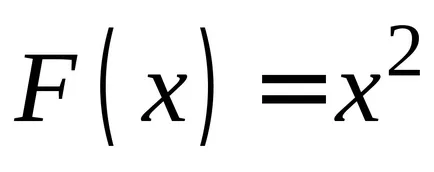
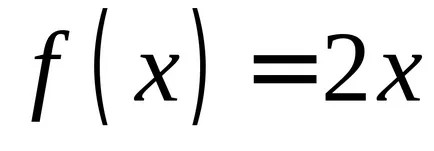
Ако установите, производните на функциите
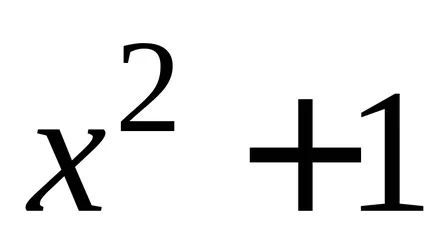
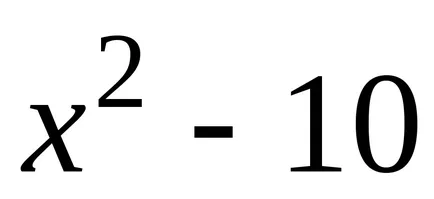
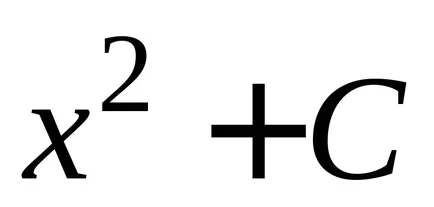

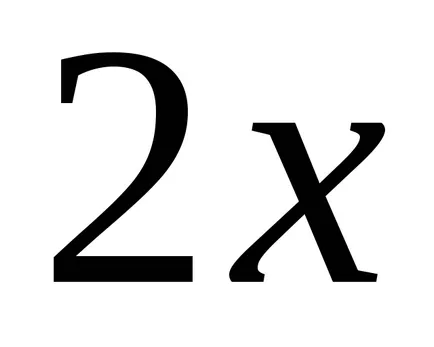
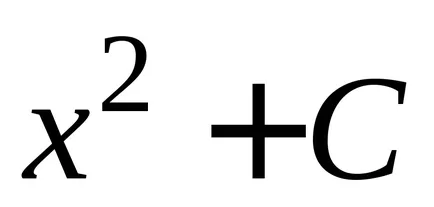
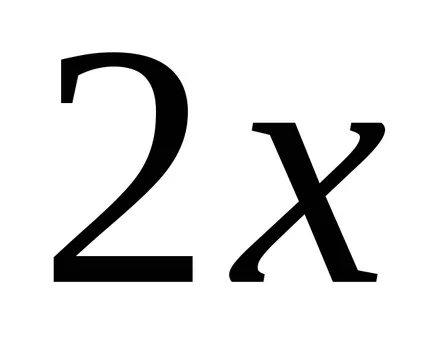
Теорема 2. Всяка непрекъсната функция има безкраен брой примитиви, както и всеки две от тях се различават един от друг само по постоянен мандат.
Да предположим, че функцията
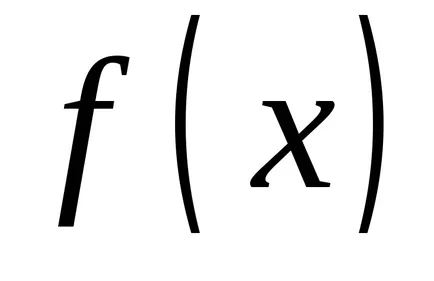
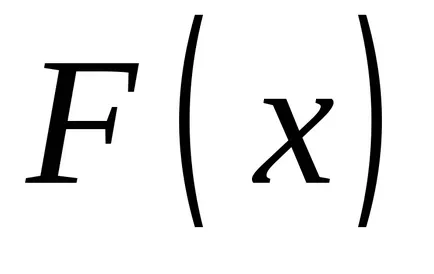
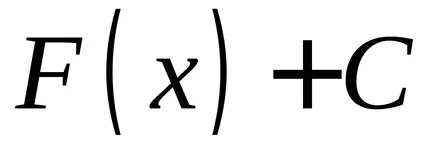

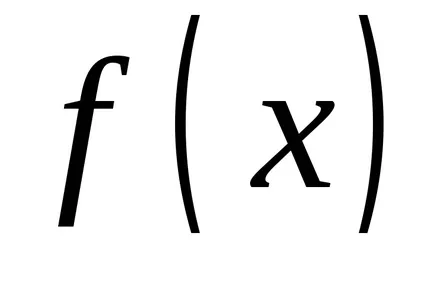
Нека функция
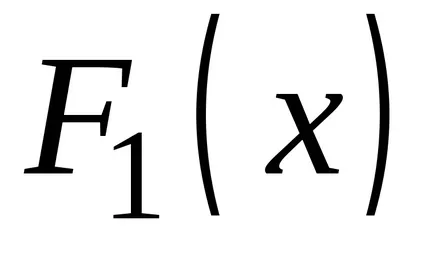
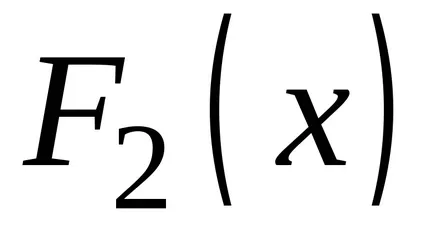
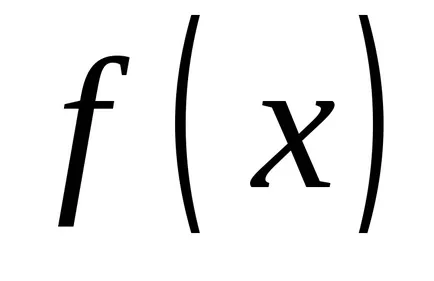
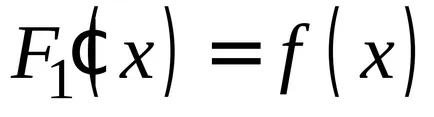
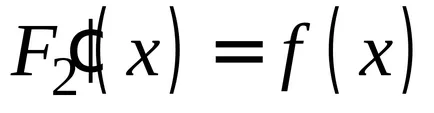
OPREDELENIE.Sovokupnost всички примитиви за подинтегрален се нарича неопределен интеграл.
В неопределен интеграл също е посочена като специфична, само без граници, т.е. ако
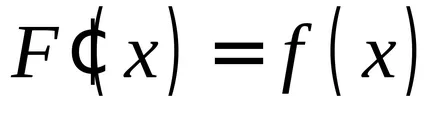
.
и

,
,
.
График примитивна функция
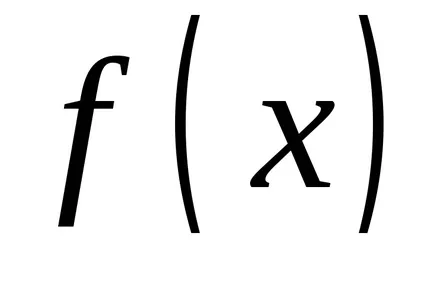
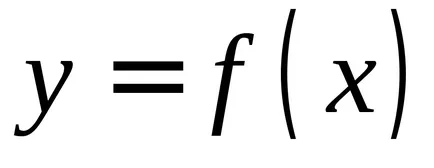
От определението на неопределен интеграл като множество от примитиви
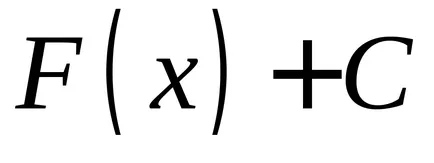
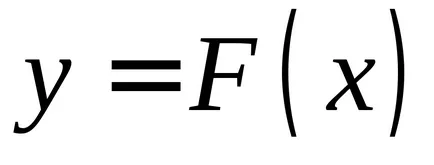

Таблица 1 показва производни и основните примитивите за елементарни функции.