симетрична разлика

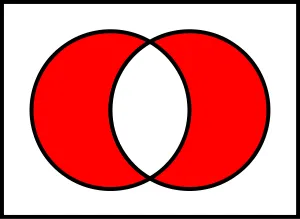
Симетричната разликата на две групи - операцията набор теорията, което води до нов набор, съдържащ всички елементи на първоначалния комплект не принадлежат едновременно както на оригиналния набор. С други думи, ако има две групи $А$ и $B$, тяхната симетрична разлика е на Съюза на елементите $А$, извън $B$, с елементи $B$, които не са членки $А$. Писмото за обозначаване на симетрична разлика на масиви $А$ и $B$ наименованието $A\; \backslash \; bigtriangleup\; B$, по-рядко използван наименование $A\; \backslash ,\; \backslash \; точка\; \backslash ,\; B$.

дефиниция

Symmetric разлика може да се влезе по два начина:

• симетрична разлика от две дадени комплекти $А$ и $B$ - е набор от $A\; \backslash \; bigtriangleup\; B$, която включва всички елементи на първия сет, които не са включени във втория сет, а също и елементите на втория сет, които не са включени в първата група:

$A\; \backslash \; bigtriangleup\; B\; =\; \backslash \; ляво\; (A\; \backslash \; setminus\; B\; \backslash \; вдясно)\; \backslash \; чаша\; \backslash \; ляв\; (B\; \backslash \; setminus\; A\; \backslash \; вдясно).$

• симетрична разлика от две дадени комплекти $А$ и $B$ - е набор от $A\; \backslash \; bigtriangleup\; B$, която включва всички елементи от двете групи, които не са общи за двете определени набори.

$A\; \backslash \; bigtriangleup\; B\; =\; \backslash \; ляво\; (A\; \backslash \; чаша\; B\; \backslash \; вдясно)\; \backslash \; setminus\; \backslash \; ляво\; (A\; \backslash \; капачка\; B\; \backslash \; вдясно).$

Концепцията може да се обобщи с симетрична разлика от броя на групите, по-голям от две.

• Симетричната разликата е двойна работа по всеки Булева;
• Симетричната разликата пътува.

$А\; \backslash \; bigtriangleup\; B\; =\; B\; \backslash ,\; \backslash \; триъгълник\; \backslash ,\; А;$

• симетрична разлика асоциативната The.

$\backslash \; Наляво\; (А\; \backslash \; bigtriangleup\; B\; \backslash \; дясно)\; \backslash ,\; \backslash \; триъгълник\; \backslash ,\; С\; =\; A\; \backslash \; bigtriangleup\; \backslash \; наляво\; (B\; \backslash ,\; \backslash \; триъгълник\; \backslash ,\; С\; \backslash \; дясно);$

• Пресечната точка на разпределителни над симетрична разлика:

$А\; \backslash \; капачка\; \backslash \; наляво\; (B\; \backslash \; bigtriangleup\; С\; \backslash \; дясно)\; =\; \backslash \; ляво\; (A\; \backslash \; капачка\; B\; \backslash \; дясно)\; \backslash \; bigtriangleup\; \backslash \; ляво\; (A\; \backslash \; капачка\; С\; \backslash \; дясно);$

• В празното множество е неутрален елемент на симетричен разликата:

$А\; \backslash \; bigtriangleup\; \backslash \; varnothing\; =\; A;$

• Всеки върна към себе си по отношение на симетрична операция разлика:

$А\; \backslash \; bigtriangleup\; А\; =\; \backslash \; varnothing;$

• По-специално, Булева операцията с симетрична разлика е абелева група;
• Булева със симетричен операция разлика също е линейно пространство над $\backslash \; Mathbb\_2.$
• По-специално, булева операция пресичане и определя симетрична разлика е, алгебра единица.
• $\backslash \; Left\; (A\_1\; \backslash \; капачка\; A\_2\; \backslash \; вдясно)\; \backslash \; bigtriangleup\; \backslash \; ляв\; (B\_1\; \backslash \; капачка\; B\_2\; \backslash \; вдясно)\; \backslash \; подмножество\; \backslash \; ляв\; (A\_1\; \backslash \; bigtriangleup\; B\_1\; \backslash \; вдясно)\; \backslash \; чаша\; \backslash \; ляв\; (A\_2\; \backslash \; bigtriangleup\; B\_2\; \backslash \; дясно);$
• $\backslash \; Left\; (A\_1\; \backslash \; чаша\; A\_2\; \backslash \; вдясно)\; \backslash \; bigtriangleup\; \backslash \; наляво\; (B\_1\; \backslash \; чаша\; B\_2\; \backslash \; вдясно)\; \backslash \; подмножество\; \backslash \; ляв\; (A\_1\; \backslash \; bigtriangleup\; B\_1\; \backslash \; вдясно)\; \backslash \; чаша\; \backslash \; ляв\; (A\_2\; \backslash \; bigtriangleup\; B\_2\; \backslash \; дясно);$
• $\backslash \; Left\; (A\_1\; \backslash \; setminus\; A\_2\; \backslash \; вдясно)\; \backslash \; bigtriangleup\; \backslash \; ляв\; (B\_1\; \backslash \; setminus\; B\_2\; \backslash \; вдясно)\; \backslash \; подмножество\; \backslash \; наляво\; (A\_1\; \backslash \; bigtriangleup\; B\_1\; \backslash \; вдясно)\; \backslash \; чаша\; \backslash \; ляв\; (A\_2\; \backslash \; bigtriangleup\; B\_2\; \backslash \; дясно);$

• Ако ролята на "сумата" играе симетрична операция разлика, както и "продукт" - на кръстовището на декорите. след комплекти образуват пръстен с единица. И други основни операции на теория на множествата, разликата между сдружението и може да се изрази чрез тях:

$A\; \backslash \; чаша\; B\; =\; A\; \backslash \; bigtriangleup\; B\; \backslash \; bigtriangleup\; \backslash \; ляво\; (A\; \backslash \; капачка\; B\; \backslash \; вдясно),$ $A\; \backslash \; setminus\; B\; =\; A\; \backslash \; bigtriangleup\; \backslash \; ляво\; (A\; \backslash \; капачка\; B\; \backslash \; вдясно).$

• Комбинирането с пресечната точка на симетричен разликата от два комплекта е на Съюза на наборите от първоначалната

$(А\; \backslash \; bigtriangleup\; В)\; \backslash \; чаша\; (A\; \backslash \; капачка\; B)\; =\; A\; \backslash \; чаша\; B$

литература