съединение интерес

Съединение интерес се нарича в смисъл, че се случва, когато натрупването на печалбите и интерес, в резултат на което лихви се увеличават по експоненциален графика. Повечето съвременни банки вземат депозити от клиенти е под сложна лихва, което несъмнено е от полза за инвеститора. Важността на откритието на сложна лихва оценяват дори самия Айнщайн, като го нарече главния "движещата сила в света."

За да разберем по-добре какво представлява сложна лихва, трябва да отидете в примерите на изчисленията.

Как да се изчисли сложна лихва?

За да се изчисли една проста формула се използва:

Във формулата за SUM се има предвид размера на окончателно споразумение с клиента при инвестиции X суми, под N - брой периоди за таксуване. В диаграмата можете да видите какво се разбира под експоненциално нарастване в размер на:

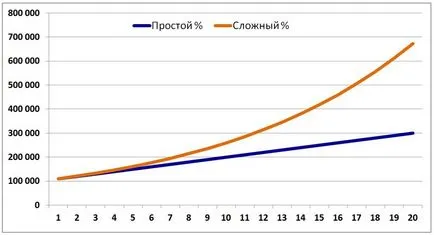
формула е малко по-трудно за банкови депозити, като въвежда нов елемент в уравнението - Капитализация:

Така че, ние трябва да знаем процентът на капитализация. Съгласно главни букви се разбира преизчисли размера на която се изчислява интерес - печалбата се добавя към основния размер. натрупани по време на последния период. Ако преизчисляване се прави месечно, капитализация честота (в тази формула е D) е 30 дни, ако е веднъж на тримесечие - 90 дни.

Останалите неизвестните параметри във формулата за изчисляване на сложна лихва банка - това е Y - броя на дните в годината (365 или 366) и P - лихвения процент. Цялата стойност на единица, след като устройството под скобата се нарича коефициент на лихвения процент.

Citizen и поставя 100,000 рубли под 15% годишно с месечна капитализация. Колко той ще бъде в състояние да се измъкне сам 8 години:

А) проста лихва?

В) със съединение интерес?

Така че, ние очакваме първия прост процент. 15% от 100,000 рубли е 15000 рубли. Ако 15 хиляди. Рубли, умножено по 8, можете да получите печалба от депозита от 120 хил. Рубли. По този начин, след 8 години гражданите и да бъде в състояние да се оттегли 220 хил. Рубли.

За изчисляване на сложната лихва, заместваме данните във формулата:

Резултатът от изчислението трябва неприятна изненада - печалба в размер на същите 120 хиляди рубли .. След това се опитайте да се изчисли размерът на годишната капитализация, вместо на месечна:

Ние получаваме резултат, който ще ни задоволи много повече - 306 000 печалба .. Ние стигаме до извода: по-малко да се появят капитализация, толкова по-висока печалба. Лихвата се изчислява на годишна база, както следва: