Решение на системи за неравнопоставеността в линейни графично
системни ограничения такъв проблем е неравенството в две променливи:
и обективната функция се прилага чрез F = C1x + C2y. искате да увеличите.
Отговори на въпроса, които чифт числа (х; у) е решение на системата, т.е. отговарят всяка от неравенството в същото време ..? С други думи, какво означава да се реши системата графично?
Първо трябва да се разбере какво е решението на линейна неравенство в две неизвестни.
Решаване на линейни неравенство в две неизвестни - това означава да се идентифицират всички двойки от неизвестни стойности, за които притежава неравенството.
Например, неравенството 3x - 5, у ≥ 42 отговарят на двойката (х г.). (100, 2); (3, -10), и така нататък. D. Задачата е да се намерят всички двойки.
Да разгледаме следните две неравенства: брадва + от ≤ в. брадва + от ≥ С. Директен брадва + с = с разделя равнината на две полуравнина, така че координатите на точките на един от тях отговарят брадва + от> С. и друга неравенство ос + + от
За определеност, нека LT 0, Ь> 0, C> 0. Всички точки с абсциса x0. лежащ над Р (например, точка М) имат YM> Y0. и всички точки, лежащи под точка стр x0 абсцисата. имат ин 
Фигура 1 Неравенството знак в половината зависи от номер. б. в.
Това предполага следния метод на графични решения на системи линейни неравенства в две променливи. За решаването на системата трябва да:
- За всеки напише неравенство уравнение, съответстваща на това неравенство.
- Изграждане на директна, е графика, функции, определени от уравнения.
- За всяка линия за определяне на полу-равнина, която се определя от неравенството. За да направите това, вземете произволна точка не лежи на права линия, за да замени нейните координати в неравенството. ако неравенството е вярно, тогава времето на равнината, съдържаща избраната точка, и разтвор на първоначалния несъответствие. При извършване на неправилна неравенство, полуравнината от другата страна е пряк набор от решения на неравенството.
- За решаването на системата от неравенства, е необходимо да се намери на площ от пресичане на половин самолети, които са решаването на всяка система на неравенство.
Тази област може да бъде празен, тогава системата на неравенството няма решение, е в противоречие. В противен случай, те казват, че системата е в съответствие.
Вземане може да бъде краен брой, и безкрайна. Районът може да бъде затворен полигон или да бъде неограничен.
Нека разгледаме три подходящи примери.
Пример 1: решаване графично системата:
х + у - 1 ≤ 0;
-2 х - 2y + 5 ≤ 0.
решение:
- разгледа уравнение х + у -1 = 0 и -2x - 2y + 5 = 0, съответстващи неравенства;
- изграждане на линии, определени от тези уравнения.

Фигура 2
Ние определяме половина-попита неравенства. Вземете произволна точка, нека (0, 0). Да разгледаме х + у 1 0, замествайки точката (0, 0): 0 + с 0 - 1 ≤ 0. Така, в половината равнина, която съдържа точката (0, 0), х + у 1 ≤ 0, ТЕ , половината равнина, разположена под линията, е разтвор на първия неравенството. Заместването на точка (0, 0), към втори, получаване -2 # 8729; 0 - 2, # 8729; 0 + 5 ≤ 0, т.е. в половината където точката е (0, 0), -2x - 2y + 5≥ 0, и се обърнахме където -2x - 2y + 5 ≤ 0, а оттам и за другата половина равнина - с това, че над линията.
Ние намираме пресечната точка на тези две половини равнини. Линиите са успоредни, така че самолетът никога не се пресичат, което прави системата неравенства данни не е несъвместимо.
Пример 2. Виж графичните решения на неравенството:
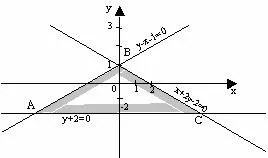
Фигура 3
1. Ние пишем уравненията, съответстващи на неравенствата и изграждане права.
х + 2y - 2 = 0