Разтворът от уравнения с параметри

Урок 2 квадратно уравнение с параметри

Урок 3 уравнения с параметри, за да бъде решен с теоремата на Wyeth

Урок 4 Разрешаване на проблеми с параметри. Extreme.

Урок 5 Разрешаване на проблеми с параметри. Функция.

Урок 6 Решение на неравенството с параметри

Урок 7 Решение на уравнения с параметри

Урок 8 системи от уравнения и неравенства

Уроци 10 уравнения с параметри и модул

Урок 11 Един експоненциално уравнение с параметър

Урок 12 тригонометрични уравнения с параметър

Урок уравнение 13 Върни параметър

Урок 14 Решението на уравнение с параметъра с помощта на производно.

Урок 15 Графично разтвор от уравнения с параметър.

Урок 16 нерационално неравенство с параметър.

Урок 17 Разтворът на модула и параметъра с помощта на геометрични тълкуване.

Урок 18 Принципът на необходимост и достатъчност при решаване на проблеми, свързани с параметри.

Урок 19 Решението на рационални неравенства с параметър.

Урок 20 Решението на уравнение с параметър съдържащ корена

Урок Фокус: линейни уравнения с параметри.

Уравнения, съдържащи в допълнение към непознати, а дори и буквални стойности се наричат уравнения с параметри. Математически структура (уравнение неравенство система, множество), съдържащ, в допълнение към неизвестното, и повече буквени стойности се наричат структурни параметри. Например уравнение AX = б е проста линейно уравнение, и в зависимост от съотношението на коефициентите А и В са три възможни случаи: ако е нула и б е нула, и ако не е равна на нула и ако е нула и б не е нула. Той обикновено се смята за две продукции с параметрите на проблема. Първата постановка. За всяка възможна стойност на параметъра или параметрите за намиране на всички разтвори предварително определени математически структура, например, да се реши неравенството Hvostov 2 <1. Вторая постановка. Найти все значения параметра или параметров, при каждом из которых решение математической структуры удовлетворяет заданным условиям, например, найти все значения параметра а при которых система уравнений не имеет решений.

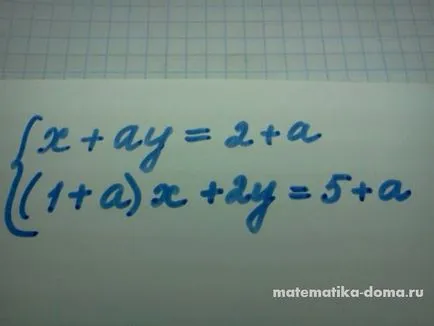
Сложността на решаване на математически структури с параметри е, че промяната в параметъра може да се промени не само коефициентите на структурите, но и ОДЗ, както и видовете, методите и техниките решения.

Линейни уравнения с параметри

Линейни уравнения, написани в общ вид, се счита за едно уравнение с параметри, например, ах = б, където х - неизвестен, а б е, така наречената параметри. Като цяло, всеки уравнение за определен параметър или референтната стойност е тази, при която изчезва за неизвестно фактор.

При решаването на линейното уравнение с случаите на параметрите счита, в който параметърът е до известна определена стойност за всеки от уравнения и тези, които се различават от него.

Специфична стойност на параметъра и обикновено е стойността на а = 0.

Помислете за решаването на следните уравнения.

1. решаване на уравнение брадва = б.