разпределителни криви - Статистически основи

Кривата, която отразява модела на промяна на честотата се нарича кривата на разпределение.

криви на разпределение са емпирични и теоретични.

Кривата на емпирична разпределение се основава на резултатите от групи (разпределение на многоъгълник).

Емпиричните крива на разпределението на първата черта (производителността на капитала) е показан на фигура 11.

Фигура 11 - емпирични разпределение кривата на функцията производителността на капитала на

Символи: х - функция стойност, е - честота

Емпирична крива на разпределението на втория характеристика (стойност на активи) е показана на Фигура 12.

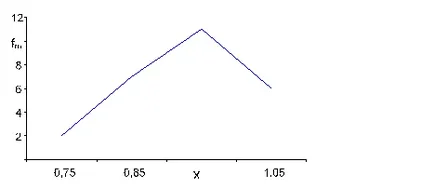
Фигура 12 - Емпиричната разпределението на характерната стойност на ДМА

х - функция стойност;

Емпирични криви на разпределение са построени на средите на диапазони.

Теоретичната крива се базира на теоретически честоти, които се изчисляват по формулата 20.

Резултатите от теоретичните изчисления за първи честота характеристика (производителността на капитала) са представени в таблица 10.

където - теоретичната честота за определена група;

- сумата от редица емпирични честоти;

- стандартното отклонение за групирани данни;

- математическа функция, определена от специални таблици в съответствие с изчислената стойност;

- I-средата на интервала;

- претеглена средноаритметично;

Таблица 10 - Изчислете теоретична честота производителността на характеристика на капитала

Теоретична честота са тези, които биха били, ако това разпределение е точно последвано нормално разпределение.

Теоретична крива на разпределението на първата функция (капитал производителност) е показана на Фигура 13.

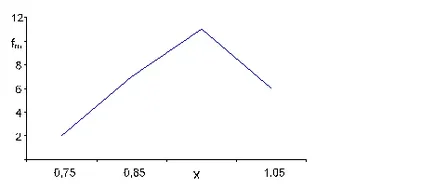
Фигура 13 - Теоретичната разпределението на производителността на капитала функция

х - среден интервал

е т - теоретична честота

Резултатите от теоретично изчисление за втората честота характеристика (стойност на активи) са представени в Таблица 11.

Таблица 12 - изчислява теоретичната честота характеристика стойност на активите

Теоретична крива на разпределението на втория характеристика (стойност на активи) е показана на Фигура 14.

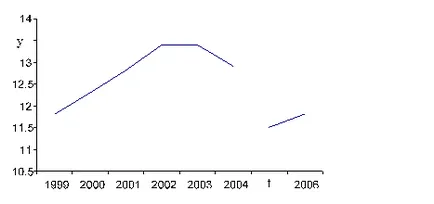
Фигура 14 - Теоретично разпределение характерна стойност на ДМА

х - среден интервал

е т - теоретична честота