Прогнозите като случайни величини, безплатни курсови работи, есета и дисертации
Получената оценка е специален случай на случайна променлива. Причината е, че комбинацията от стойностите на пробата случайно, защото - случайна променлива и следователно, е случайна променлива и нейните функционални комплект стойности. Вземете, например, - оценка на очакването:
По-горе показва, че стойността в тия наблюдение могат да се разделят на два компонента: постоянна част и чисто случаен компонент:
където - пробата средни стойности.
От това можем да видим, че ...
Също така има и фиксирани и чисто произволни компоненти. Нейната фиксиран компонент - това е, очакването, и неговата случаен компонент - това е, средната стойност на чисто случаен компонент в пробата.
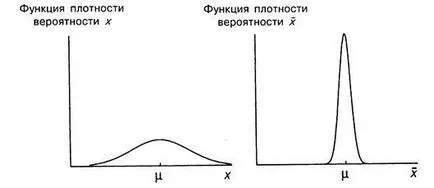
функция плътност на вероятностите и за същите са показани на графиките (фиг. A.6). Както е показано на фигурата, стойността се счита за нормално разпределение. Тя може да се види, че разпределението, както и симетрични по отношение на - теоретичната средната за страната. Разликата между тях е, че разпределението е вече по-висока. Стойността вероятно трябва да бъде по-близо до от една стойност наблюдение, тъй като неговата случаен компонент е средно аритметично от чисто случайни компоненти в пробата, която очевидно "гасят" помежду си при изчисляване на средната за страната. След това теоретичната стойност на дисперсията е само част от теоретичната дисперсия.