Предизвикателства за използването на Питагоровата теорема
Когато сте само началото, за да научите квадратни корени и начини за решаване на ирационални уравнения (уравнения, съдържащи неизвестно под знака корен), е по-вероятно да се получи първо впечатление за тяхното практическо приложение. Възможността да се извлече корен квадратен от номера е необходимо да се решават проблемите при прилагането на Питагоровата теорема. Тази теорема отнася дължините на страните на всеки правоъгълен триъгълник.
Нека дължината на краката на правоъгълен триъгълник (двете страни, които отговарят на под прав ъгъл), за да бъдат определени от букви и дължина на хипотенузата (най-дългата страна на триъгълника срещу десен ъгъл) е обозначен с буквата. Тогава за съответен период са свързани, както следва:
(Сумата от квадратите на краката на правоъгълен триъгълник е равен на квадрата на дължината на неговата хипотенуза).
Това уравнение позволява да се намери дължината на страните на правоъгълен триъгълник в случаите, когато известната дължина на другите две страни. Нещо повече, тя позволява да се определи дали триъгълника в процес на разглеждане правоъгълни, с уговорката, че дължините на трите страни са предварително известни.
Разтворът на проблеми с помощта на Питагоровата теорема
За укрепване на материала ще реши следните проблеми при прилагането на Питагоровата теорема.
Задача 1. С помощта на данните, посочени по-долу дължини на страните на правоъгълен триъгълник, изчисли дължината на другите страни.

- Дължината на един от краката е равно на 48, хипотенузата - 80.
- дължина крак е 84, хипотенузата - 91.
Започваме да адрес:
а) данни заместване в уравнението дадени по-горе дава следните резултати:
48 2 + 2 б = 80 2
2304 + б 2 = 6400
Тъй като дължината страна на триъгълника могат да бъдат изразени с отрицателна стойност, второто изпълнение автоматично изхвърля.
Отговорът на първо теглене: б = 64.
б) дължината на втората част на триъгълника е по същия начин:
84 2 + 2 б = 91 2
7056 + б 2 = 8281
Както и в предишния случай, отрицателното решение се изхвърли.
Отговорът на второ теглене: б = 35
Задача 2. С помощта на данните, посочени по-долу на дългите страни на триъгълници, определи дали те са правоъгълни.
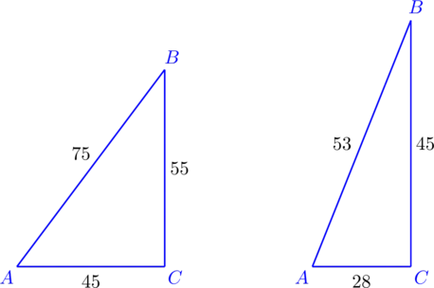
- Дължината на малки триъгълни страни са 45 и 55 съответно, по - 75.
- Дължината на малки триъгълни страни са 28 и 45 съответно, повече - 53.
а) необходимостта да се провери, е дали сумата от квадратите на дължините на страните на триъгълник квадрата на дължината на по-малката още:
45 2 + 55 2 = 2025 + 3025 = 5050
Следователно първата триъгълник не е правоъгълна.
б) Изпълнение на същата операция:
28 2 + 45 2 = 784 + 2025 = 2809
Следователно второто триъгълника е правоъгълна.
Задача 3. дадена точка (-2, -3), (2, 1), (5, -2) в правоъгълна координатна система в равнината. Разберете, ако те са върховете на правоъгълен триъгълник.
Първо, ние откриваме, максималната дължина на сегмента, образувана от точките с координатите (-2, -3) и (5, -2). За това се използва познатата формула за намиране на разстоянието между две точки в правоъгълна координатна система:
По същия начин, ние откриваме, дължина на сегмент между точките с координати (-2, -3) и (2, 1):
Накрая се определи дължината на отсечката между точките с координати (2, 1) и (5 -2):
От уравнението притежава:
съответния триъгълник е правоъгълна.
Така, че е възможно да се формулира отговор на проблема: тъй като сумата от квадратите на страните с най-малка дължина е равна на квадрата на страната с най-голяма дължина, точки са върховете на правоъгълен триъгълник.
Проблем 4: изграждане на портите на момчето Ваня. В разгара те трябва да достигне два метра ширина - три. Ако приемем, че ъглите образувани от постовете, ще има пряко, това, което ще бъде дължината на кабела протегна диагонално от единия ъгъл до друг?
Първи (разположен хоризонтално), опора (разположени вертикално) и кабел (опъната диагонално) образуват правоъгълен триъгълник, съответно, да се намери дължината на кабела може да се използва от Питагоровата теорема:
По този начин, дължина на кабела ще бъде около 3.6 метра.
Задача 5. Момчето Vite, изисквана за измерване на ширината на езерото. Откри разстоянието от точка R на точки P и Q, са разположени на противоположните страни на басейна, както е показано по-долу, и се увери, че ъгъл Р - линия. Ако приемем, че изчисленията са верни, това, което е дължината на езерото от запад на изток?

Предвид: разстояние от точка R точка Р (триъгълник крака) е равна на 24, от точка до точка R Q (хипотенуза) - 26.
Така че, да помогне за решаването на проблема с Vita. От двете страни на триъгълника, изобразен на фигура вероятно образуват правоъгълен триъгълник, за да открие трета страна може да използва дължината на питагорова теорема:
По този начин, на ширината на езерото е 10 метра.