площ на полигон, programmirovanie-DLA-sshool
Урок от серията "Геометрични алгоритми"
Добре дошли, скъпи читателю.
Решаването на много проблеми на компютърната геометрия тя се основава на намирането на площта на многоъгълник. В този урок ние извлече формула за изчисляване на площта на полигона на координатите на върховете му, пише функцията за изчисляване на площада.
Задача. Изчислете площта на многоъгълник. дал координатите на върховете му, за да ги избегне на часовниковата стрелка.
Информация от компютърната геометрия
За да се извлече района на полигон, ние се нуждаем от информация изчислителна геометрия, а именно, концепция, ориентирани към зоната на триъгълника на.
Ориентирано площ на триъгълника - това е обща зона, оборудвана с знак. Знак на триъгълник ABC ориентирана Районът е същата като тази на ориентирани ъгълът между векторите и. Това означава, че неговата знак зависи от реда на прехвърляне на възли.
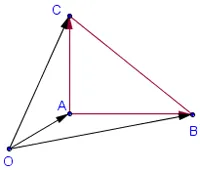
Фиг. Правоъгълна - 1 триъгълник ABC. Площта му е ориентирана (това е по-голяма от нула, като двойката е ориентирана позитивно). Същата стойност може да бъде изчислена по друг начин.
Нека A - произволна точка на самолета. В нашата рисунка площ на триъгълник ABC се получава, ако площта на триъгълник OBC изваждаме области ОАВ и ЗЗД на. По този начин, можете просто да добавите до областите на триъгълници ориентирани свръхактивен пикочен мехур, OBC и ЗЗД. Това правило работи за всеки избор на точката О.
По същия начин, за да се изчисли площта на всеки полигон да се прибират ориентирани области на триъгълника
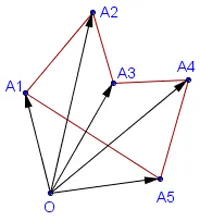
Накратко, тя се превръща района на полигон, взето със знак плюс, ако е лявата (заобикаляйки граница обратно на часовниковата стрелка), и със знак минус, ако е на дясно (кръг по часовниковата стрелка), когато пресичат наклонени многоъгълник.
По този начин, изчисляване на площи полигон намалена до намирането на площта на триъгълник. Нека да видим как да го изразя с координатите.
вектор продукта от два вектора в равнината е площта на успоредник конструирана на тези вектори.
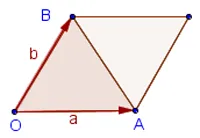
Вектор продукт, изразена по отношение на координатите на векторите:
площ на триъгълник е равен на половината от тази област:
Като точка O, която е да се вземат на произхода, а след това на координатите на векторите, по които се изчислява целевата зона, равна на координатите на точките.
Нека (x1 y1.), (X2 y2.), ..., (Xn, ин) - координати на върховете на многоъгълника, с цел заобикаляне или обратно на часовниковата стрелка. След това ще бъде ориентирано S е площта на:
Това е нашата формула работи, тя се използва в нашата програма.
Ако координатите на върховете са уточнени в пропускане на обратно на часовниковата стрелка, числата S, изчислени в съответствие с тази формула, той ще бъде положителен. В противен случай, той ще бъде отрицателен, а за обичайната геометрична област ние Req-Димо поеме своята абсолютна стойност.
Така че, помислете за програмата, за да се намери областта на полигон, определена от координатите на върховете.
Vertex координати чете от input.pas файл. се съхраняват в масив А под формата на две нива. За удобство, многоъгълника се вписват в прекосява масив п + 1 елементи, чиято стойност е равна на първия елемент масив.
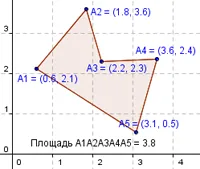
вход:
5
0,6 2,1 1,8 3,6 2,2 2,3 3,6 2,4 3,1 0,5
Imprint:
S = 3.91
Ще се видим в следващия урок.