Питагорова теорема, триъгълници

Питагорова теорема в геометрията не е по-малко важно от таблицата за умножение по аритметика. Разтворът на много геометрични проблеми (като в планиметрия и в твърда геометрия), се редуцира до разглежда използването на правилните правоъгълен триъгълник и това забележително теорема.

В правоъгълен триъгълник, на квадрата на хипотенузата е равен на сбора от квадратите на другите две страни.

Има много различни начини, за да докажат, Питагоровата теорема. Ние се ограничаваме само до един от тях.

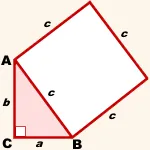
Нека BC = а, AC = б, AB = с.

На хипотенузата AB изграждане на квадрат със страна С.

В продължението на страничната АС отложи AF сегмент, AF = а,

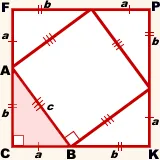
за разширяване на тази част от BC - сегмент BK, BK = б.

CF = AF + AC = а + б, СК = BC + BK = а + б, т.е. CF = CK = а + б.

Чрез точките F и К прекарват линии, успоредни на крака на триъгълник:

Четиристранната CFPK - успоредник (по дефиниция).

И тъй като ∠C = 90 ° и CF = CK, на CFPK - квадрат със страна а + б.

Тъй като площта на квадрат е равно на квадрата на едната си страна,

От друга страна, район CFPK е равна на сумата от площите на четири правоъгълен триъгълник с крака Б и В и квадрат със страна в.

площ на квадрат със страна с е равен на c².

Приравняването на дясната страна на формули CFPK повърхности:

След опростяване получаваме

QED.

Тъй като краката на правоъгълен триъгълник е най-често по-нататък а и б. и хипотенузата - както в, тогава формула питагорова теорема обикновено написан така: