Определяне на координатите на няколко места, Хансен задача линейно ъглов удар класификация

задача Хансен

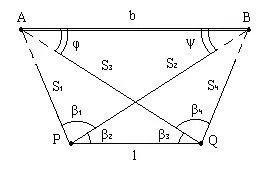
Проблемът с Hansen са координатите на две точки P и Q от известните координатите на две точки А и В и четирите ъгъла, измерени при дефинирани точки (ris.2.15), което означава, че проблемът е Hansen двойна обратна връзка ъгъл изрез.

Първоначална информация: XA, YA, XB, YB.

Измерените елементи: В1, В2, В3, В4.

Неизвестни елемента: XP, YP, XQ, YQ.

Graphics решение. Mark два листа прозрачна хартия (проследяване на хартия) и изграждане на ъглите им: на един лист - ъглите В1 и В2, от друга листа - ъгъл B3 и В4. Нанесете върху чертежа (план или карта) двата листа и да ги движи в произволен начин да се съчетаят посока ъгли на тези листове с букви А и Б в чертежа. Perekolot точки P и Q в чертежа.

Аналитичен решение. Има няколко начина за решаване на проблема на Хансен; резюме от тях.

За да реши проблема с обратна между точките А и В, а именно, изчисли дължината на сегмента б КБ и азимут направления Баб АБ.

Въвеждане на произволна единица дължина, равна на интервала на дължина L PQ; L = 1.000.

Изчислява сегменти S'1 = AP, S'3 = AQ, S'2 = BP, S'4 = BQ в произволни единици при използване на първи синусова теорема за триъгълник PAQ, след това за PBQ триъгълник:

Изчислете дължина единици б "на сегмента AB на триъгълник QAB на косинус:

и да се контролира - от PAB триъгълник:

И двете стойности трябва да съвпадат.

Изчислете коефициента к:

и прехвърлят всичките изчисляват разстояния в реалната единица дължина:

Изчислете ъгъла на Fi QAB триъгълника на косинус:

Изчислете ъгъл w на триъгълника PAB за косинус:

Изчисляват азимут посока AQ:

и решаване на проблема с права геодезична точка А до точка В:

Изчислява посока азимут на BP BBP BBA = - п и решаване на проблема с права геодезически точка В до точка Р:

Местоположение изходни точки и точките могат да бъдат определени така, че сегментите PQ и AB пресичат (фигура 2.16); хода на решаване на проблема остава един и същ, само за промяна на предназначението на ъглите и страните. Освен това се оказа, че в това изпълнение, позициите на точки P и Q се определят няколко пъти по-точно отколкото в общата изпълнение.

Единичната проблема Хансен не контролни измервания, така че на практика на четирите ъгъла на измерванията не се ограничават до, и да извършват по-нататъшни измервания.

Линейно-ъглова инсулт

Класификация на линейни и ъглови движения

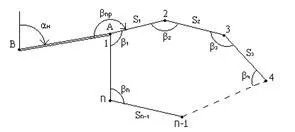
За определяне на координатите на няколко места може да се прилагат различни методи; най-често срещаните от тях са линейно-ъглова удар, системата на линейни и ъглови движения, триангулация, трилатерация и др. Линейно ъглов удар представлява последователност полярен сериф където измерените хоризонтални ъгли и разстоянието между съседни точки (фигура 2.17).

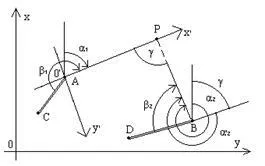
Първоначалните данни в линейно време на ъгловите координати са XA, YA точки А и азимут BBA линия BA, който се нарича с посока на ъгъла на първоначалния източник; този ъгъл може да бъде посочено безусловно чрез координатите на точка В.

Измерените стойности - хоризонтален ъгъл В1, В2. ВК-1 и ВК разстояния S1, S2, SK-1, SK. Също известен грешка измерване ъгъл MW и относително измерване на разстояние грешка Ms / S = 1 / T.

Посока Гарнитура инсулт ъгли последователно изчисляват от известен предаване формули чрез азимутния ъгъл на въртене

за ляв ъгъл. (2.64)

за прав ъгъл. (2.65)

За да включите Фигура 2.17 имаме:

Координати на точките, получени от процеса на решаване на пряк проблем geodezichekoy първата от точка А до точка 2, а след това от точка 2 до точка 3, и така нататък до края на своя страна.

Линейно ъглов удар, изобразена на фигура 2.17, е много рядко се използва, тъй като няма контрол на измерване; На практика, като правило, се прилага удара, което осигурява такъв контрол.

Оформете и пълнота на първоначалните данни е линейно-ъглова инсулти се делят на следните типове:

Open игрище (Фигура 2-18): изходни точки с известни координати и първоначалната азимут от там в началото и в края на хода на буталото;

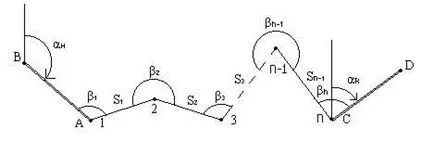
2.18. Шофиране с отворен ъгъл линеен инсулт

Ако в началото или в края на удара не е оригиналната азимут, тя ще се премести на непълно работно нарязаната; Ако източникът на насочени ъгли в ни най-малко, той ще работи с пълен нарязаната.

затворен линейно-ъглова инсулт (ris.2.19) - начални и крайни точки на удар се обединяват; една точка инсулт има известни координати и се нарича отправна точка; На този етап трябва да бъде на стартовата линия с известна посока ъгъл, и измерва primychny ъгълът между тази посока и по посока на втория параграф на инсулт.

Ris.2.19. Схема затворен линейно ъглов удар

Висяща линейно-ъглова инсулт (фигура 2.17) е началната точка на известно местоположение и първоначалната азимут само в началото на завоя.

безплатно линейно-ъглова инсулт не е отправна точка и първоначалната посока ъгли или в началото или в края на курса.

Според точност на измерване на хоризонтални ъгли и разстояния линейно-ъглова инсулти се разделят на две основни групи: теодолит движения и poligonometricheskih ходове.

В теодолит канали хоризонтални ъгли са измерени с грешка от не повече от 30 ", относителното разстояние грешка MS измервателните / S варира от 1/1000 до 1/3000.

В poligonometricheskih канали хоризонтални ъгли са измерени с грешка от 0.4 "до 10", и относителната грешка на измерване Ms / S разстояние е от 1/5000 до 1/300 000. Чрез измерване точност poligonometricheskih пасажи са разделени в два бита и четири класа (вж. Раздел 7.1).