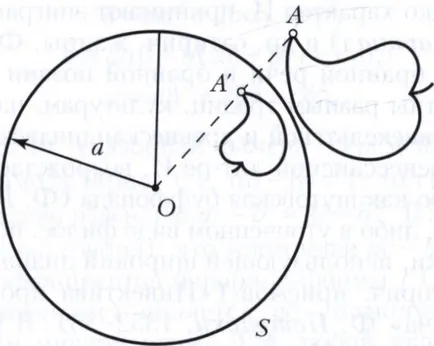
Инверсия в трансформация математика равнина, в която точка О, който се нарича инверсия център, фиксирани и всяка точка А, не съвпада с О, преминава към точка А "лежи на линията OA, така че продуктът от дължините на отсечки ОА и ОА" е някои брой к, еднакви за всяка точка А (фиг.). За центъра на инверсия понякога се нарича полюс инверсия и к - степен или съотношение инверсия. Точки S окръжност с център О и радиус √k премине под инверсия в себе си; изображения външни за S точки са вътрешни точки, както и вътрешни образи - външни; център на инверсия не е изображение. Понякога това се нарича инверсия симетрия по отношение на кръга. Ние също така да обмислят инверсия к<0. Инверсия с отрицательным коэффициентом k равносильна инверсии с тем же центром О и положительным коэффициентом |k|, сопровождаемой симметрией относительно точки О. Инверсия с k> 0 се нарича хиперболичен и с к <0 - эллиптической инверсией или антиинверсией.
Линията, минаваща през центъра на инверсия се трансформира в себе си. Права линия не минаваща през центъра на инверсия се трансформира в кръг без една точка. Този кръг минава през точка О и точка O е изключен от кръга, обратното също е вярно. Кръгът перпендикулярна на окръжност с център О и радиус √ | к |, се превръща в себе си. В декартови координати, инверсия центриран в основата може да бъде определена чрез формулите
или в комплекс равнина с формула Z '= к / Z, където лентата означава комплекс конюгиране.
Подобно инверсия на обхвата, определен в пространството.
Инверсия трансформация от 1824 систематично прилага швейцарски математик J. Щайнер.
сродни статии
← Обратни генетика
Инверсия в лингвистиката →