Образователна прилагане на числени методи за апроксимация на функция

метод кубически шпонки

Произходът на термина "шпонките" е свързан с гъвкава линия чертеж, който се използва за изготвянето гладки криви, преминаващи през дадените точки.

Сплайн интерполация - бърз, ефективен и устойчив начин на интерполация функции. Заедно с рационално интерполация, сплайн интерполация е полином интерполация на алтернативи [28].

интерполация на база сплайн въз основа на следния принцип. интерполация интервал е разделен на малки сегменти, всеки от които се определя от полином функция от трета степен. Коефициентите на полинома са избрани така, че да отговарят на определени условия (което зависи от метода на интерполация). Общото за всички видове изисквания на трети ред сплайн - непрекъснатост и, разбира се, преминаването през точките възложени. Допълнителни изисквания може да бъде линейна функция между възли, непрекъснатостта на висшите производни и т.н.

Основните предимства на интерполация на шлицов е неговата стабилност и ниска сложност. Линейно уравнение система, която трябва да бъде решен за конструиране шпонки, много добре инсталация, която позволява да се получи коефициентите на полиномите с висока точност. В резултат на това, дори и за много голяма изчислителна схема N не губи стабилност. Изграждане на маса коефициент сплайн изисква O (N) операции, както и изчисляване на стойността на шлицови в даден момент - само

Обикновено кубичен полином шлицов избран за

дефинирана в интервала.

Цялата кривата е набор от кубически полиноми (фигура 1.4) с правилно избраните коефициенти - параметър шлицов [20, 38].

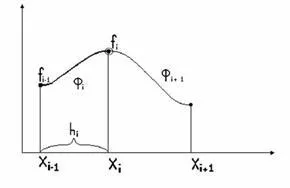
Фигура 1.4: Схема шпонки методи

Коефициентите за всеки интервал се определя от условията на предаване в възли:

В допълнение, на границата, когато са определени условията и

Ние търсим един кубичен полином под формата

От условието имаме

и изискват приемственост си в.

Общият брой на неизвестните коефициенти очевидно е равен. броят на уравнения (1.13) и (1.14) е равна. Липсва две уравнения, които получаваме от (1.12) за ф.

Експресия (1.14). Заместването на този израз в (1.13) и с изключение на. получаваме:

Сега заместване на изрази за първия + във формула (1.14), след прости трансформации за определяне на втория уравнение за разлика:

С граничните условия:

И условието е еквивалентно на уравнението. Уравнението на разлика (1.15) с условията (1.16) може да бъде решен чрез метод на почистване, представени като система от линейни алгебрични уравнения на формата. където векторът съответства на вектора. вектор F е елемент стрелка дясната страна на уравнение (1.15) и матрица А има следната форма:

помете метод, въз основа на предположението, че неизвестни неизвестни са свързани с отношението на повторение:

С помощта на тази връзка, ние можем да изразим и чрез замени и аз-е уравнение:

където - от дясната страна на уравнението-тото. Тази връзка ще се извършват независимо от решението, ако е необходимо:

От първото уравнение получаваме:

След намирането и progonochnyh коефициенти. като се използва уравнение (1) до получаване на разтвор на системата. В същото време,

Шпонка интерполация е добре, защото това изисква познаване на само възлите на функцията, но не и неговите производни [34, 36, 43].