Натежителна разделителен нормална форма се нарича дизюнкцията на всички implicants представляваща намалената система

Deadlock DNF- експресия, получени от намалената DNF, допълнително опростяване е невъзможно в DNP.

Минимална DNF DNF нарича безизходица, която се състои от най-малкият брой букви.

Същото съкращение DNF може да има няколко безизходица DNF DNF и няколко минимум.

Процесът на минимизиране на първия етап се редуцира до конструиране пълни implicants система, тогава понижено материал implicants система, която е изработена от съкратена DNP след конструирана сляп DNP и след това до минимум DNP избран. Решение на проблема се извършва в съответствие със схемата,

Получаване на кондензираната DNP (намиране implicants функция).

Получаването съкратен DNP въз основа на лепене на закона. От това следва, че е възможно да се залепи или да се слеят mintermy, различаващи се само от един от факторите. Ние няма да се държим заедно mintermy и комплекти. Нека да запишете всички набори от променливи, съответстващи mintermam в рамките на функциите на разширяване в колони, като ги разделя на групи, така че всяка група се състои от комплекти с еднакъв брой единици.

Разходите свързване в двойка набори от съседни групи (за залепване комплекти трябва да се различават от една променлива). Когато лепене на общи елементи са запазени, както и елементи, които определят различават заменя линия. Комплекти, участващи в свързване са отбелязани с *. Това води до втората колона, до която също се прилага операцията по свързване. Така лепило групи от съседни групи с една и съща позиция на тирета. Освен образува трето колона и т.н. Процесът продължава, докато свързването е възможно.

Implicants функции са набори от всички колони не са участвали в свързване (не е отбелязана).

Съкратено DNF. дължината му е 17 знака

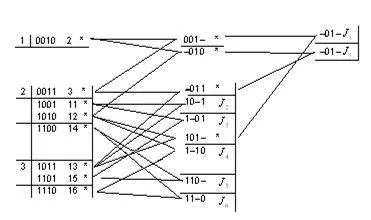
Фиг. изобразени implicants и залепени набори от променливи.

Имайте предвид, че тази цифра показва броя на масивите в осмична.

2. Следващата стъпка - изграждане на безизходица DNF. За да направите това, трябва да се направи implikantnuyu маса. Редовете на таблицата отбелязани implicants функции и колони mintermami функция. Всеки implicant е част от дизюнктивен член PDNF и единство със същия набор, както съответстващото minterm. Пресечната точка на линия, в която се записва implicant и колони съответстващ mintermov, част от който е implicant, достави кръстоски. Натежителна форма е дизюнкция на тези implicants, които покриват всички mintermy, т.е. В таблицата можете да изберете следните редове към всички колони са имали поне един предимство.

Да се ​​изгради форма безизходица, вие трябва да изберете минималния брой линии, покриващи кръстовете всички колони. Ясно е, че в избраната система редове трябва задължително включва редове, съдържащи плюсове, които са само в колоната. Тези линии се наричат ​​основни. Прости implicants стоящи в основни линии, формират ядрото на функцията. Кръгът професионалистите в редовете, съответстващи на тези implicants. От останалите implicants изберете минималния брой, така че покритието пресича всички свободни колони (т.е., тези, които не съдържат).

DNF В безизходица трябва да включва. в противен случай първите две колони, не се покриват. Следователно, първият ред е основно и implicant образува основните функции. Когато този избор се ограничава автоматично и още две колони. задънени implicants

Рисунката показва цялата безизходица DNF:

Сред всички безизходица DNF DNF изберете най-малката дължина:

метод Матрица на Карно.

метод матрица се основава на някои геометрични конструкции. Съотношението между двоични променливи могат да бъдат представени по ясен геометрична форма.

Помислете за логика функция на две променливи. Всички четири от съчетаването на два бинарни променливи (членове PDNF) може да се опише по равнина под формата на точки с координати 00,01,10,11, където първата цифра съответства на променливата. а вторият - променлива. Тези точки могат да бъдат свързани чрез линии и получената квадрата е визуално изобразяват членове PDNF две променливи.

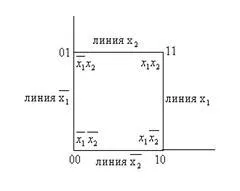
Координати на върховете на квадрата, отбелязани двоични числа, съответстващи на двоични номера на съюзи. 00 sotvetstvuet. 01 -. 10 -. 11 -. Координати на съседни върха различават само от един двоичен цифров и следователно mintermy съответстващи на тези номера са различни само една променлива. Ако комбинирате условията, съответстващи на два различни върхове, тази променлива ще бъдат изключени. Например, нагъване и mintermy. изобразен върхове 00 и 01, ще получим едно =. същата операция изключение променлива може да се извърши директно чрез сравняване на две двоични числа 00 и 01.V първа цифра двоични цифри и в двете числа са равни, обаче в Съюза, 0, знаците са различни във втория ред освобождаване от отговорност, така настроен през втората изхвърлянето.

Броят 0 е променлива. Таблото показва, че променливата е изключено. Ето защо, ако две двоични числа се различават нули и единици, само в един разряд, те могат да се заменят с двоично число, което в тази малко можете да поставите тире. Тире показва броя на изключените променлива. Линията, свързваща върховете 00 и 01 може да се нарече линия.

Геометрична модел функция на три променливи може да служи като триизмерен куб, чиито върхове съответства на условията, PDNF. Координатите на съседните върхове са различни, както в случая с плосък модел, само едно двоично, и на съответните членове на само една променлива. В резултат на това на линията, свързваща съседните върховете на куба може да се опише с две променливи, които не променят смисъла си на линията, както и лицата на куба - една променлива.

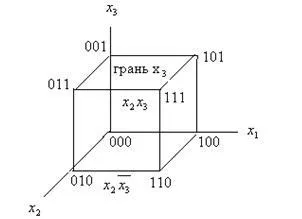
Свързването на две съседни върхове линия елиминира една променлива, и това изключение може да се направи чрез сравняване на двойна система за означаване на върховете. Например, сравняване на 011 и 111, получаваме. която съответства на работата на добавяне съюзи

По подобен начин съединение 4 линии върхове лежи в една и съща страна, премахва две променливи. Наистина, сравняване на 011 до 111 и 001 до 101, получаваме

Първоначално променливата бе изключен. и след това променлива.

В резултат на това имаше една променлива.

За функцията на четири променливи геометричен модел е четириизмерен куб. Въпреки това, за да го представят в самолета и не може да се използва, за да сведе до минимум трудно. По-удобно да се минимизира карта Karnaugh. Karnaugh карта е конструиран така, че две съседни колони (редове) се различават от един символ. Всяка връзка от четири променливи е представена на картата, като една клетка се намира в пресечната точка на редове и колони, които формират двоична бройна система броят на връзка. Съюзи съответстващи на съседните клетки се различават само една променлива. В непосредствена близост до Карно карта не само клетки, присъстващи в картата, но също така и в краищата на всеки ред и всяка колона. Всяка функция може да се намира на единици на сензора в клетките в съответните PDNF съюзи - mintermam и нули в останалите клетки, които не могат да бъдат записани. Например, функцията има единици в клетки, 0000, 0001.1100, 1101. Четири minterma могат да бъдат групирани в две комбиниране на тази съседна mintermy. Обединени mintermy контури на затворени линии. В резултат на функцията е сумата на двата съюза на три променливи.

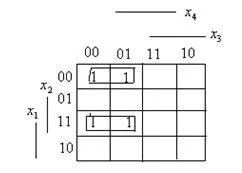
В резултат на това ние получаваме минимизиране функция

Преобразуване извършва на Karnaugh карта отговарят на следното алгебрични манипулация

Ще се обадим на конфигурацията, образуван от съседни клетки, пълни, под-малките квадрати. От под - набор от клетки, в които един или повече променливи са постоянни. По този начин, според картата на четирите променливи за площад две клетка се характеризира с факта, че има три променливи константа, четвърти приема и двете им стойности. За tetrachoric на под постоянни две променливи, а другите двама да предприеме всички четири възможни комбинации от стойности. Комбинирането на две съседни клетки, като по този начин ние ще се изключи една променлива, съчетаващ четирите съседни клетки, премахване на две променливи чрез комбиниране на осем съседни клетки - изключва три променливи. (Това е вярно в случай, когато формата на суб е правоъгълна или квадратна). Клетките могат да бъдат комбинирани под-малките квадрати, които са в различни краища на ред или колона.

Пример. 2. Да предположим, че даден Karnaugh карта.

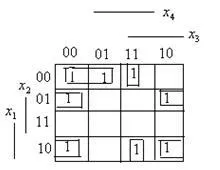
2. Да предположим, че даден Karnaugh карта.

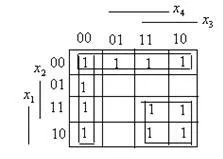
В резултат на това ще сведе до минимум на функцията