Намери непълнолетните и кофактори на елементите на алфа - документът - страница

намерите непълнолетните и алгебрични α12 елементи допълнения. α32. Изчислява детерминанта: а) разширяване на елементите на първия ред, а втората колона; б) получаване на предварително нули в първия ред.

Cofactors на А12 елементите и A32 са съответно:

а) Изчисляваме определящ фактор, тя се разширява върху елементите на първия ред:

+ = 1 - 3 (8 + 2 + 4 - 4) - 2 (- 8 - 16 + 6 + 12 + 4 - 16) + (16 - 12 - - 4 + 32) = 38;

Разширяваме детерминанта от елементите на втората колона:

= - 2 - 2 + 1 = - 2 (- 8 + 6 - 16 + + 12 + 4 - 16) - 2 (12 + 6 - 6 - 16) + (- 6 + 16-12 - 4), = 38;

б) изчисляване на получените предварителни нули в първия ред. Ние използваме съответната собственост на детерминанти. Увеличаването на третата колона 3 детерминанта и се добавя към първия и след това се умножава по -2 и се добавя към втората. След това, в първия ред на всички елементи, с изключение на един, ще бъде нула. По този начин ние се разлагат, получена детерминанта от елементите на първия ред и да го изчисли:

(В детерминанта на третия ред получи нули в първата колона на същите като посочените по-горе свойства на детерминанти.) ◄

Дадено ни система от линейни нехомогенни алгебрични уравнения

Проверете дали системата е в съответствие, в случай на съвместимост да се реши: а) по правило Крамър; б) като се използва обратна матрица (метод матрица); в) метод на Гаус.

►Sovmestnost проверка на система от теоремата на Кронекер - Капели. Използването на елементарни преобразувания намери ранга на матрицата

Тази система и рангът на разширената матрица

За тази цел ние умножаване на първия ред на матрица B -2 и се добавя към втората, и след това се размножават първия ред до -3, и се добавя трета, обмен на втория и третия колони. получаваме

Следователно позвъни А = ранг В = 3 (т. Е. Броят на неизвестни). Така че, на оригиналната система е последователна и има уникално решение.

а) по правило Крамър

б) за намиране на решения на системата с помощта на обратна матрица напиши системата от уравнения в матрица форма Ах =. Разтвор на системата в матрична форма е х = А-1. Според формула намираме обратен матрицата А-1 (което съществува, тъй = Det А = - 16 ≠ 0):

в) решаване на системата на метода на Гаус. X изключат от втора и трета уравнения. За тази цел, първото уравнение умножим по 2 и се изважда от втори, следван от умножаване на първото уравнение с 3 събиране и изваждане на третата:

От получената система находката х = - 4, у = 1, Z = -2. ◄

Върховете на пирамидите са в точки А (2; 3; 4), В (4; 7; 3), C (1, 2, 2) и D (- 2, 0, - 1). Изчислете: а) площ от лицето на ABC; б) площта на напречното сечение, която преминава през центъра на ребрата АВ. AC. АД; в) обемът на ABCD пирамида.

►a) Известно е, че SABC =. Намираме: = (2; 4 - 1)

б) Междинен AB ребра. BC и AD се намира в точките (3, 5, 3,5)

F на сила = (2; 3-5), приложена към точка А (1 - 2 2). Изчислява: а) работна сила F, когато на мястото на приложението му, движещи се праволинейно премества от положение А до положение В (1; 4; 0); б) единица момент на сила F по отношение на точка Б.

Известни върхове г (0, 0), А (- 2, 0) на OASD на успоредник и пресечната точка на диагоналите на (2; -2). Напишете уравненията на страните на успоредник.

►Uravnenie ръка ОА може да се запише едновременно: у = 0. Освен това, тъй като точка Б е средата на диагоналната АД, чрез разделяне на сегмент в две формули може да се изчисли координатите на връх г (х, у) (Фиг. 1):

Вече можете да намерите най-уравнения на всички други страни. Като се има предвид сходството на ОА и CD посоки. Ние образуват страна на уравнение CD: у = -4. страна на уравнение OD се състои от две известни точки:

И накрая, ние намираме уравнението страна AC. предвид факта. че да преминава през известен точка А (- 2, 0) паралелно известен директно OD:

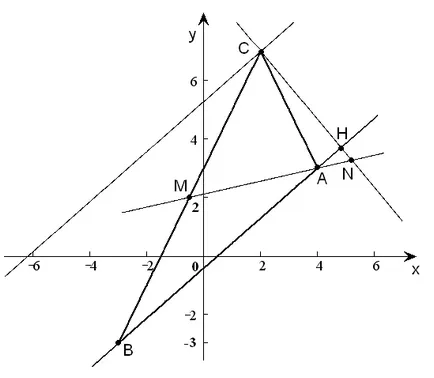
а) уравнение AB страна;

б) височина уравнение CH на;

б) средната уравнение AM;

ж) точката на пресичане N AM и средната височина СН;

д) уравнението на линия, минаваща през връх С, успоредна на страната AB на;

д) разстоянието от точка С до линията AB.

►a) С помощта на уравнението на правата линия, минаваща през две точки. получаваме страната от уравнението AB:

б) Съгласно уравнението

в) Чрез добре познати формули намираме координатите на х. Y средната М на сегмент пр:

Сега за две известни точки А и М форма Медианата на уравнение на:

ж) За координатите на точката на пресичане N AM и средната височина CH съставяне на системата от уравнения

Решаването това, ние получаваме N (26/5; 49/15);

г) След линия, минаваща през връх С, успоредна на страната AB. техните ъглови коефициенти са k1 = 6/7. След това, в съответствие с уравнението:

д) разстоянието от точка С до линията AB се изчислява при използване на известни формула:

Решението на този проблем е илюстрирано на фиг. 2 ◄

►a) Използване на равнина уравнение с три точки. образуват уравнение A1A2A3 равнината на:

където 6x - 7V - 9z + 97 = 0;

б) Като се има предвид уравнението на линията, минаваща през двете точки. A1A2 директен уравнение може да се запише като

в) От състоянието на перпендикулярност pryamoyA4Mi ploskostiA1A2A3 следва, че като посока вектора на линията и може да нормалата п = (6 - 7-9) A1A2A3 равнина. Тогава уравнението на линията A4M като се вземат предвид каноничните уравнения на права линия може да се запише като

г) Съгласно формулата за намиране на ъгъла между правата линия и равнината

д) В съответствие с формула намиране на ъгъла между равнините

Уравнението на равнината, минаваща през точка М (4; 3; 1) и

N (- 2, 0, - 1), успоредни на линията изтегля през точки А (1, 1, - 1) и

►Soglasno формула прави уравнения в пространството. минаваща през две точки, уравнение права линия има формата AB

Ако равнина преминава през точка М (4; 3; 1). уравнението може да бъде записано като А (х- 4) + B (у 3) + C (z- 1) = 0. От тази равнина и преминава през точка N (- 2, 0, - 1). Тогава условието

А (- 2-4) + В (0-3) + С (- 1 - 1) = 0 или 6А + 3B + 2С = 0.

Тъй желаната равнина е успоредна на линията намерено AB. след това при спазване на условията на формулите на успоредните линии и самолети, ние имаме:

-4А + 0B + 1C = 0 или 4А - С = 0.

откриваме, че С = 4А, В = -А. Заместването на получените стойности на С и В в желаната равнина уравнение, получаваме

Тъй като ≠ 0. получената уравнение еквивалент на уравнението

3 (х - 4) - 14 (у - 3) + 12 (Z - 1) = 0. ◄

►Zapishem параметрични уравнения на правата линия M1M2. перпендикулярна на тази равнина: х = 6 + т, у = - 4 + т, Z = - 2 + т. решаването им с уравнение дадена равнина, ние получаваме т = 1 и следователно директно точка на пресичане M1M2 М на тази равнина с: M (7 - 3; - 1). Тъй като точката М е средната точка на сегмента M1M2. истинското равенство

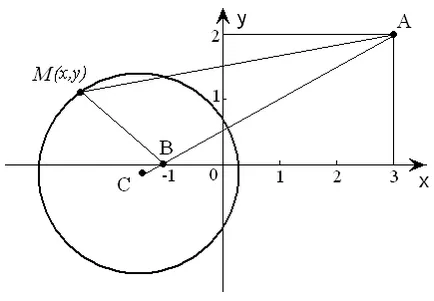
Уравнението на линия, всяка точка М на която е разположена на разстояние от точка

А (3, 2) на разстояние от три пъти по-голям от този, от точка В (- 1, 0).

►Pust М (х; у) - всяка точка на желаната линия (Фигура 3.). След това, от състоянието на проблема | AM | = 3 | BM | , защото

след уравнението на необходимата линия

Ние го трансформира чрез повишаване на двете страни на площада. В момента има:

Отбелязването на пълните площади в последното уравнение, получаваме уравнението на формата

който е уравнението на окръжност с център в точка

Създаване на каноничните уравнения: а) елипса, на полуос А е равно на 3. В центъра на вниманието е точка F (0); б) с въображаемата ос на хиперболата, фокусът на 2. и F (-, 0); в) парабола с директриса х = -3.

►a) Canonical уравнение има формата на елипса. Съгласно изложението на проблем голяма полуос на а = 3, р =. За елипса, равенството

б) каноничен уравнение има формата на хипербола. Чрез хипотеза въображаема ос б = 2 и С =. За хипербола равенство b2 = c2-А2. Следователно А2 = с2-B2 = () 2- 22 = 9. запис желания хипербола уравнение:

в) каноничен уравнението на параболата в този случай трябва да бъде на формуляра У2 = 2px. и директриса уравнение х = - р / 2. Но състояние уравнение проблем директриса х = - 3. Следователно - р / 2 = - р = 3. 6 и необходимия каноничен уравнение има формата на парабола

Свързани документи:

детерминанта naytiminory и algebraicheskiedopolneniyaelementov AI2. това от елементите и-ти ред. 3; 7; -5), В (2, -4, 1). Задача 7 има предвид два вектора: = <8; 4; 1>, = <2;–2; 1>. Намери вектор. и копланарни вектори. перпендикулярна на вектора.

намери квадратна матрица) minorelementa; б) algebraicheskoedopolnenieelementa; в). Намерете) minorelementa; б) algebraicheskoedopolnenieelementa; в) детерминанта, от предшестващото нули в първия ред. Решение: а) Minoromelementa.

елемент матрица. " Определение. Algebraicheskimdopolneniemelementa aіk матрица се нарича Мала МИК тази матрица, умножена по (1) и + за: Algebraicheskoedopolnenieelementa. метод. Пример 1. Виж дадена матрица Det A. разтвор. Transform.

тата колона; наречен minoromelementa. След това, по дефиниция, счита (1) - algebraicheskoedopolnenieelementa. след това (2). Линейни операции с матрици задача. Намерете сбора на матрици и продукта. съвместим, той е длъжен да намери своето общо решение.

Този фактор се нарича minoromelementa Aij. Определени Мала - MIJ. Пример: За Naytiminorelementa детерминанта А12. на единица по-долу и Мала е: Algebraicheskimdopolneniemelementa детерминанта се нарича непълнолетен взела със себе си.