Наборът от рационални числа, най-големите проучвания портални

Наборът от рационални числа

В допълнение към рационални числа, има редица различно естество - те често водят до работата на извличане на корен квадратен (и не само те, но ние с теб, че не знам). Така че, ние трябва да се по-задълбочено запознаване с нови номера. но
първо да се опитаме да организираме нашите знания за "старите", т.е.. д. по-рационално, номера.

1. Някои от символите на математически език

Вие сте добре известен с естествени числа:
1, 2, 3, 4.
Наборът от всички числа общо означена с буквата N.
Ако прикрепен към естествени числа от 0 и всички отрицателни числа: -1, -2, -3, -4. - получавате набор от числа. Този комплект обикновено е обозначен с буквата Z.
Ако набор от цели числа, за да се свържете всички общи части: .. и така нататък - вие получавате много ratsinalnyh номера. Този комплект обикновено се означава с буквата Q.
Всяко число m могат да бъдат написани като фракция. Следователно, твърдението, че зададената Q на рационални числа - е набор от номера на формата
С помощта на тази нотация N, Z, Q, приемате следното:
1. Вместо фразата "п - естествено число", можете да напишете (да се чете: "елемент принадлежи на снимачната площадка н N»), математически символи, наречени знак за принадлежност.
2. Вместо фраза «M - число" можете да напишете м Z.
3. Вместо фразата «Р - рационално число", можете да напишете р Р.
Ясно е, че N - част от серия Z и Z - част от комплект Q. За описание на ситуацията в областта на математиката и специална нотация:

Математически символ за да активирате позивна (един набор в друг).
Като цяло, по математика за запис х X означава, че X - е един от елементите на X. Записът означава, че зададете е подмножество на V. математика често казваме: А - подмножество

Моля, обърнете внимание: наборите по математика обикновено са обозначени с главни букви, както и елементите на комплекта - малки букви.
И за миг, бележка подписва аксесоари (т принадлежи) и включване (един комплект се съдържа в друга) - най-различни, съответно
Рекорден така х принадлежи на набор Х или, че А не е част (подгрупа) на множеството B? Те използват едни и същи герои, но пресича с наклонена черта :.
Ето няколко примера за използване на математически символи, въведени за краткост истински математически твърдения - също като верни твърдения.

2. рационални числа като безкрайни периодични десети

За рационални числа, както вече нееднократно е подчертавал, са всички тези числа, които успешно сте оперирани до тогава, докато той се срещна с квадратни корени.
Те са цели числа, общи части, десетични.
Поради всички тези номера, можете да използвате един и същ метод за запис, което ние сега обсъдим.
Да разгледаме например, цяло число 5, общата фракция и десетична дроб 8377. 5 число могат да бъдат написани като безкрайна десетична дроб: 5,0000. Десетична дроб 8377 също може да бъде записано като безкрайна десетична дроб: 8,377000. За да използвате метода на
"Ъгъл участък":

Както можете да видите от втория цифри след настъпване десетичната запетая повторение на една и съща група от номера: 18, 18, 18. По този начин,
= 0.3181818. Накратко тя се изписва така: 0.3 (18). Повтаряне група на знака след десетичната точка се нарича период и много знак - периодично безкраен десетична дроб.
периодичен безкраен десетична дроб. За да направите това, в периода на запис на 0:
5 = 5,00000. = 5 (0). Същото е и с броя 8377: 8377 = 8,377000. = 8377 (0).
За да запазите нещата подредено, да кажем: 8377 - краен десетични и 8,377000. - безкрайна десетична.
По този начин, броят 5 и номера. а броят на 8377 може да бъде записан под формата на безкрайна периодична десетична дроб.
По принцип всяко рационално число може да се запише като безкрайна периодична десетична дроб.

Забележка. Това заключение е полезна за теорията, но не толкова удобно за практика. В крайна сметка, ако даден краен десетична дроб 8377, тогава защо
влизането му под формата на 8377 (0)? Ето защо, обикновено казват: всяко рационално число може да се запише като краен десетични, или под формата на безкрайно
солна периодична десетична дроб.
Над показахме как един обикновен фракция представени под формата на безкрайна периодична десетична. Обратно, всеки периодичен безкраен десетична дроб може да бъде представена като обща част. Това означава, че всяка безкрайна десетична дроб периодично там
рационално число.
Ние показваме пример как периодично безкраен десетична дроб се превръща в обикновен фракция.

Пример. Добави към една обща част периодично безкраен десетична дроб: а) 1 (23); б) 1.5 (23).
Разтвор) Нека х = 1, (23), т. Е. X = 1,232323.
Умножаваме х от редица такива, че запетаята е преместен в дясно от точно един период. Тъй като периодът съдържа две числа трябва да запетая премества надясно с две цифри, и този брой х да се умножи по 100.

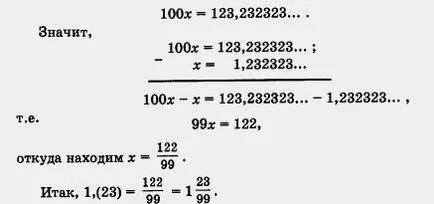
б) Комплект х = 1,5 (23) = 1,5232323. Първо, ние умножи х с 10 за работа в получения период започва веднага след десетичната запетая: 10x = 15.232323. Сега умножете броя на 10x 100 - тогава запетая промяна от точно един период на дясно: 1000x - 1523,232323. имаме

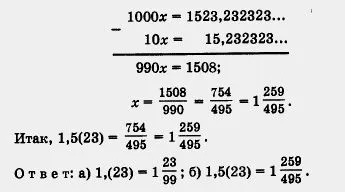
Сега ние заявяваме основният резултат от този раздел: настройте Q на рационални числа може да се мисли като набор от номера на формата.

където m - е цяло число, п - цяло число, или като множество периодични безкрайни десети.