Мобиус лента, платформа съдържание

Чернова Анна Николаевна

Цел: Всеки от нас има интуитивен представа за това, което "повърхността". Повърхността на лист хартия, повърхност клас стенна повърхност на света са известни за всички. Възможно ли е - нещо неочаквано и дори загадъчна по такъв конвенционалната концепция? Пример Мобиус лента показва, че е възможно.

1. Какво е лентата на Мьобиус?

2.Veliky математик - астроном.

4. Как да направите Мобиус лента.

5. Колко стени ще има по-Мобиус съблича?

6. Soldatik- Changeling.

Какво е лентата на Мьобиус?

Топология е необходимо математици почти всички специалности, много е красиво, си метод, в сравнение с други едновременно с това предоставят по-широк, по-мощни и по-прости теореми.

Лентата на Мьобиус е много лесно да се направи, държат в ръцете си, да се намали, за да експериментирате като нищо друго. Проучване на Мьобиус ивица - едно добро въведение в елементите на топологията: теорема на Ойлер, оцветяване, гъвкавост, идеята за непрекъснато съпоставяне.

Close "странно" геометрична обект е бутилката Клайн. Klein бутилка може да се получи чрез свързване на две Мьобиус ленти по ръбовете. В конвенционален триизмерно евклидово пространство, за да направите това без да се създава самостоятелно кръстовища, не е възможно.

Други подобни резултати - реалната проективна равнина. Ако пробивния отвор в реалния проективна равнина, а след това, което е останало е Мьобиус ивица. От друга страна, ако се придържате към диска лента на Мьобиус, съчетаващ в своите граници, резултатът е проективна равнина. За да се визуализира това, че е полезно да се деформира Мьобиус ивица, така че границата му се превърна в общ кръг. Такава форма се нарича "груб шапка" (груб покритие може също да означава същата форма с лепени диск, т.е. потапяне на проективна равнина в R 3).

Налице е често срещано погрешно схващане, че грубия капак не може да се формира в три измерения, без самостоятелно пресичащи повърхност. Всъщност е възможно да се постави Мьобиус ивица в R 3 с граница, която е идеален кръг. Идеята е, както следва: - Да С е единичната окръжност в равнината х-у в R 3. Комбинирането диаметрално противоположен точка В. т.е. точката, при ъгли # 952; и # 952; + Π му дъга, получаваме, че за # 952; между 0 и пи / 2 дъги лежи над равнината на XY. за другите # 952; по-долу (и на две места дъга лежат в равнината х-у на).

Може да се отбележи, че ако дискът е прикрепена към граница кръг, самостоятелно пресечната точка на получената проективна равнина свързан в триизмерното пространство. По отношение на референтните страните на квадрата, както е показано по-горе, реалната проективна равнина се получава чрез залепване "постоянство" ориентация останалите две страни.

Как да си направим Мобиус лента.

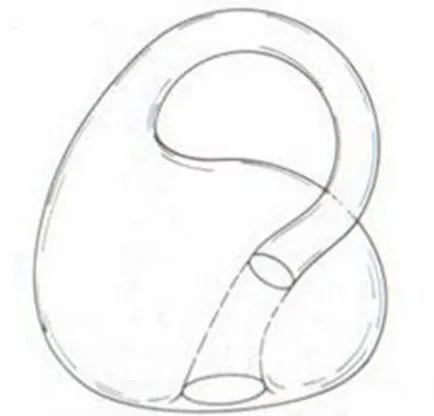
Вземете хартиена лента AVSD разрязано наполовина по ширината на пунктирана линия (вж. Фиг.) Се използва по краищата AB и CD помежду си и да се държим заедно. Но това не е толкова ужасно, както и, в точка А съвпада с точка D, и точка Б - до точка В. Ние обрат лентата веднъж преди поставяне. Оказа известен по математика хартия пръстен. Той дори има специално название - лента на Мьобиус. Сега ние нарязани на лентата с ножица залепени в средата, по протежение на пунктирана линия. Разбира се, ако не са усукани лента преди лепене всичко би било просто: един широк пръстен ще имаме две тесни. И какво сега?

Колко стени ще има по-Мобиус съблича?

В лентата, от който е направена лентата на Мьобиус, има две страни. И самият той, е само едната страна!

Нека се опитаме да рисувам Мьобиус ивица - парче по парче, без да се преминава през ръба на лентата. И какво се случи? Можете боя над цялата Мобиус ивица! "Ако някой - някога трябваше да нарисува" само едно "стронций повърхността на Мьобиус ленти, макар че е по-добре да го потопят в кофа с боя" - написана от Ричард Courant и Херберт Робинс в отлично си книга "Какво е математика."

Ако вътрешността на обичайната пръстен на паяк завод, а от външната страна - за да им позволи да лети и пълзи произволно забрана само за да се изкачи над ръба на ринга, а след това на паяка няма да можете да получите да лети. И ако и двете ги сложи на лента на Мьобиус, бедните ще бъде изяден муха, освен ако, разбира се, паяк пълзи по-бързо.

Аз изрежете войник хартия и го е изпратил по пунктираната линия, разходки в средата на ивицата Мобиус. И той се върна в началната точка. Но в каква форма! В посока нагоре надолу! И така, той се върна в началото в нормално положение, че е необходимо да се направи още една "krugolistnoe" пътуване. Проверете!

Експериментите за всеки.

Вземете лентата, разделете всяка страна на три равни ленти и лепило, усукване веднъж ивица Мобиус. Ние ще се реже по пунктирана линия. Ако лентата не е усукан, тогава първо ще съкрати един пръстен, а след това още две други. И трите пръстена, всеки от същата дължина като оригинала, но по-малко от три пъти по ширина. Но ние имаме Мобиус лента. И "не приема" ножица хартия, изрязани по пунктирани линии всичко наведнъж и да получите две преплетени пръстени. Един от тях е два пъти по-дълго, колкото на източника и усукани два пъти. Второ - Мьобиус ивица, ширината на която е три пъти по-малък от оригинала.

ЗАКЛЮЧЕНИЕ: Тази работа може да помогне на студентите да разширят

КЕН. Научих в обикновените понятия ТЪРСИ неочаквано и дори загадъчна.

1.Vneklassnaya работа по математика.

3.KRATKY OCHEREK историята на математиката. DY Struik. превод

от немски и допълнения I. B.POGREBYSSKOGO.