Линиите и равнини в пространството - studopediya

Уравнение на линия, линията на пресичане на две равнини:

Чрез всеки ред в пространството преминава безброй равнини. Всеки два от тях се пресичат и го определят в пространството. Следователно, всеки две уравнения на равнините, разгледани заедно представляват уравнението на тази линия.

Като цяло, всеки две неуспоредни равнини определени общи уравнения

Правата линия на тяхното пресичане. Тези уравнения се наричат ​​общото уравнение на линията.

уравнение на линията, минаваща през двете точки:

Ако точки данни и B лежат на една линия, успоредна направо Ox ос (y2 -U1 = 0) или ос ОУ (-H1 х2 = 0), тогава уравнението на линията ще съответно имат формата на Y = Y1 и х = x1

Пример 4. Създаване на уравнение на права линия, преминаваща през точките А (1, 2) и В (1; 1).

Решение: Заместването в уравнение (8) x1 = 1, Y 1 = 2, Х2 = 1; Y2 = 1, получаваме:
или където 2у = 4-х-1 или х-2y накрая + 3 = 0

Canonical уравнение на реда:

Нека равнината, определена правоъгълна Декартова координатна система Oxy. Ние си поставихме задачата: получаваме уравнението на линията А. ако - точка и права линия - в посока вектор на една права линия.

Да - плаваща точка на линията А. Тогава векторът е посока вектор на права линия и има координати (ако е необходимо, вижте statyunahozhdenie координати на координатите на точките). Очевидно е, че множеството от всички точки на равнината, определена права линия, минаваща през точка и с посока вектор тогава и само тогава векторите са колинеарни.

Пишем за необходимо и достатъчно условие за колинеарност на вектори. , Последното равенство в координатна форма е.

Ако. тогава можем да запишем

Получената уравнение се нарича каноничната форма в равнината уравнението на линията в правоъгълна координатна система Оху. Уравнението се нарича уравнение на права линия в канонична форма.

Така че, каноничното уравнение на линията се в масивите от гледна самолет в правоъгълна координатна система Oxy права линия, минаваща през и с посоката на вектора.

Ето един пример на каноничното уравнение на права линия в равнината.

Например, уравнението е уравнението на права линия в каноничната форма. Линия, съответстваща на това уравнение да минава през точката. и - посоката вектор. По-долу е нагледна илюстрация.

Обърнете внимание на следните важни факти:

· Ако - в посока вектор на права линия и правата линия минава през точката като. и през точката. След това му канонично уравнение може да се запише като. и;

• Ако - посоката вектора на права линия, след което всеки от векторите също посока вектор на правата линия, следователно, всеки от уравненията на права линия, която съответства на каноничен форма.

На параметрични уравнения на линията:

Теорема. В следната система от уравнения е параметри уравнение на линията:

където - координатите на фиксирана точка на линията, - съответните координати на произволна посока вектор на правата линия, т - параметър.

Доказателство. В съответствие с уравнението за определяне на всеки набор от точки на координатната пространство, ние трябва да покажем, че уравнения (7) отговарят на всички точки на линията L и, от друга страна, не отговарят на координатите на точка, която не лежи на права линия.

Нека да е произволна точка. Тогава вектори и са колинеарни, по дефиниция и от теоремата на колинеарност на два вектора, следва, че една линейна комбинация от друга, т.е. има номер. това. От равенството на векторите и равнопоставеността на техния произход:

От друга страна, нека точката. Тогава от теоремата на колинеарност на вектори никой от тях не може да бъде линейно изразена по отношение на друг, т.е. и най-малко един от уравнения (7) не е изпълнено. По този начин, уравнения (7) udovletvoryayutkoordinaty само онези точки, които се намират в права линия L, а само тези, QED

Нормалната уравнението на равнината:

В вектор форма, уравнението на равнина под формата

Ако нормалата на равнината - единична,

то уравнението на самолета може да се запише като

(Нормална равнина уравнение).

- разстояние от произхода на самолета. , - посоката уюта на нормалната

където - ъгълът между нормалната равнина и осите на координати, съответно.

Общото уравнение на равнина (8) могат да бъдат доведени до нормална умножение с коефициент нормализиране. подпише, преди отсреща изстрел към свободния член (8).

Разстоянието от точка до равнина (8) е разположен на формула получава чрез заместване на точката в нормално уравнение

Общото уравнение на равнината, изследването на общото уравнение на равнината:

Ако не е дадено на триизмерното пространство правоъгълна координатна система Oxyz. уравнението самолет в тази система е триизмерна координатна пространство, наречено уравнение с три неизвестни х. Y и Z. което е изпълнено от координатите на всички точки в равнината и не отговаря на координатите на всяка друга точка. С други думи, чрез заместване на координатите на точка в равнината уравнение на тази плоскост получаваме идентичността, а когато е заместен в уравнение координатната равнина до всяка друга точка ще фалшиво равенство.

Преди да напишете общото уравнение на равнината, ние си спомняме, определянето на права линия, перпендикулярна на равнината: директен, перпендикулярна на равнината, ако тя е перпендикулярна на всяка права линия лежи в равнината. От тази дефиниция следва, че всяка равнина, перпендикулярна на нормалата на всеки ненулев вектор лежи в равнината. Този факт ние използваме в доказателството на следната теорема, която определя формата на общото уравнение на равнината.

Всяко уравнение на формата. където AB С и D - са реални числа, при което А, В и С не са едновременно нула, определя равнина в предварително определена правоъгълна координатна система Oxyz в триизмерното пространство, и всяка равнина в правоъгълна координатна система Oxyz в триизмерното пространство се определя от уравнението определен за някои номера AB С и D.

Както можете да видите, теоремата се състои от две части. В първата част, ни се дава от уравнението и ще трябва да докаже, че той определя със самолет. Във втората част, ни е дадено на самолет и трябва да докаже, че е възможно да се определи едно уравнение за определен избор номера AV C и D.

Нека започнем с първата част от доказателството на теоремата.

Тъй като номера А, В и С не са едновременно равно на нула, тогава има точка. координатите на които отговарят на уравнението. което означава, че равенството. Изваждане на лявата и дясната страна на това уравнение, съответно, от лявата и дясната страна на уравнението. По този начин ние получаваме уравнението е еквивалентно на оригиналния уравнението. Сега, ако ние се докаже, че уравнението определя със самолет, се оказа, че еквивалентното уравнение също така определя самолет при предварително определено правоъгълна координатна система в триизмерното пространство.

Равенството е необходимо и достатъчно условие за перпендикулярност и вектори. С други думи, с плаваща запетая координати удовлетворяват уравнението и то само когато перпендикулярни вектори. След това, като се има предвид факта, споменато по-горе теорема, можем да кажем, че ако равенството. множеството от точки определя равнина, която е нормално вектор. където тази равнина преминава през точката. С други думи, уравнението определя правоъгълна система koordinatOxyz в триизмерното пространство определено над равнината. Следователно, еквивалентно уравнение определя една и съща равнина. В първата част на теоремата.

Ние се пристъпи към доказателството за втората част.

Да предположим, че са дадени равнината, минаваща през точката. нормален вектор, който е. Ще докажем, че в правоъгълна координатна система Oxyz тя определя от уравнението на формуляра.

За да направите това, ние приемаме произволна точка на самолета. Нека тази точка да бъде. След векторите са перпендикулярни и, следователно, тяхното скаларен продукт е нула :. След като вземе. уравнение става. Това уравнение определя нашия самолет. Така теоремата е напълно доказана.

Уравнението се нарича общо уравнение на равнина в правоъгълна координатна система Oxyz в триизмерното пространство.

Общото уравнение на форма равнина. където - реално число, различно от нула, определя правоъгълна координатна система Oxyz равнина съвпада с равнината. тъй като посочва един и същ набор от триизмерни точки в пространството. Например, уравнения и да посочите една и съща равнина, тъй като те отговарят на координатите на една и съща триизмерно пространство на пункта.

Малко се изясни значението на теоремата.

Предварително определената правоъгълна координатна система Oxyz равнина и общо уравнение неразривно свързани. Това означава, че всяка плоскост съответства на обща равнина уравнението на формата (с определени стойности на числата А. Б. С и D), и това уравнение съответства на споменатата предварително определена равнина в правоъгълна координатна система в триизмерното пространство.

Ето един пример, който показва последното изречение.

Погледнете рисунката на самолета в триизмерното пространство, при фиксирана правоъгълна координатна система Oxyz. Тази равнина съответства на уравнението. тъй като той е удовлетворен от координатите на всяка точка в равнината. От друга страна, уравнението определя предварително определена координатна система Oxyz набор от точки, чието изображение е показана на фигурата равнина.

Уравнението на равнината на парчета:

Да предположим, че в триизмерното пространство, посочено правоъгълна координатна система Oxyz.

В Декартова координатна система Oxyz в триизмерното пространство, уравнение на формуляра. където. б и в - не са нулеви реални числа, наречени уравнението на равнината на парчета. Това име не е случайно. Абсолютните стойности на числата а. В и С са дължините на сегментите, които равнина пресича координатните оси Ox. Oy и Oz, съответно, като се започне от произхода. Отличителни номера а. В и С показват в каква посока (положителен или отрицателен) са депозирани на интервали от координатните оси. В действителност, на координатите на точките удовлетворяват уравнението на равнината на парчета:

Вижте снимката, обяснявайки тази точка.

Уравнението на равнина, минаваща през точка перпендикулярно на вектора: Да предположим, че в определени триизмерното пространство правоъгълна Декартова координатна система. Нека формулираме следния проблем:

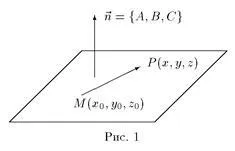
Писане ортогоналността на вектори (. → п МР) = 0 в координатна форма, ние получаваме:

Това е желания уравнение. Вектор → п = А. Б. С> се нарича нормален вектор на самолета.

По този начин, за да се напише уравнението на равнината, което трябва да знаете нормалата на равнината и всяка точка prinazhdezhaschuyu самолет.

Ако сега в уравнението (1), за да отворите на скобите и да доведе до подобни термини, ние получаваме общото уравнение на равнината:

Уравнението на равнината, минаваща през три точки:

Да предположим, че в триизмерното пространство е фиксирана правоъгълна координатна система Oxyz. той съдържа три различни точки. които не лежат на една линия. Ако следния проблем: да се напише уравнението на равнината, минаваща през тези три точки.

Ще покажем, два начина за разрешаването му.

Първият метод съставянето уравнения равнината, минаваща през три дадени точки.

Известно е, че общото уравнение от наборите на форма в равнината правоъгълна координатна система Oxyz самолет. която минава през точката. и нормалата на равнината има координати. Ето защо, ние може да получи общо уравнение на равнината, ако знаем координатите на точката, през които тя преминава, както и координатите на нормалния вектор на този самолет. От това знание и ще изгради, когато уравнението на равнината, минаваща през три дадени точки.

Така че, от условията на проблема, ние знаем координатите на точката (дори и координатите на три точки), чрез който равнината, чиито уравнение, което трябва да се направи. Остава да намерите координатите на нормалния вектор на този самолет.

Тъй нормалата на равнината, и всеки ненулев вектор, перпендикулярна на тази равнина, векторът перпендикулярна на вектора. и вектора. Следователно, като вектор, можете да вземете вектор продукта и. От ф (виж статията на изчисляването на координатите на вектора координати на точки, ако е необходимо), а след това. След изчисляване на определящ фактор записва станат нормални координати вектор видими. и може да записва желания уравнението на равнината, минаваща през три определени точки.

Вторият метод за намиране на уравнението на равнината, минаваща през три определени точки.

Очевидно е, че поставените въпроси определя правоъгълна система koordinatOxyz в триизмерното пространство, равнината, минаваща през три различни и не лежат на една права линия, точка. единствено и само ако основните елементи и копланарите.

Следователно, трябва състоянието на една равнина на три вектори. който е смесен продукт на вектори трябва да бъде нула :. Това уравнение в координатна форма е. Това е, след изчисляване на определящ фактор е общо уравнение на равнината, минаваща през три дадени точки.

Освен това, от получената общото уравнение на равнината, минаваща през три дадени точки, можете да отидете на уравнението на равнината на парчета за нормалното уравнение на равнината, ако е необходимо.

Остава да се разгледа решението на примери, в които е уравнението на равнината през три несъвпадащи и не лежат на една права линия, точка.

Разстоянието от точка до равнина:

Разстоянието от точка до равнина - е дължината на перпендикулярно от гледна точка на самолета.

Ако дадена равнина уравнение Ах + С + D + Cz = 0, разстоянието от точка М (.. Мх ми Mz) на равнината може да се намери с помощта на следната формула: