Квадратичен Форми 1

Квадратичен форма на F (.. X1 X2 хп) на п променливи се нарича сумата всеки член на която е квадратна на една от променливите, или продукта на две различни променливи, се приема с някои коефициент: F (.. X1 X2 хп) = (Aij = Aji ).

Матрица, съставена от тези коефициенти, се нарича матрица квадратна форма. Винаги е симетрична матрица (т.е. матрица, симетрично около основната диагонала, Aij = Aji).

В матрица нотация, квадратна форма F (X) = X T AX, където

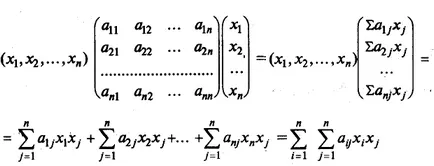
Например, квадратното форма, пишем в матрична форма.

За да направите това, ние откриваме, матрицата на квадратното форма. Нейните диагонални елементи са равни на квадратите на коефициентите на променливите, както и други елементи - Половината от съответните коефициенти на квадратното форма. следователно

Нека колона матрица променлива X получава nondegenerate линейна трансформация матрица колонна Y, т.е. X = CY, където С - неособена матрица п-ти ред. Тогава квадратна форма F (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.

По този начин, когато не-дегенеративен линейна трансформация с матрицата на квадратна форма има формата: A * = C T АС.

Например, ние откриваме квадратичен форма е (y1 y2.), Извлечени от квадратичен formyf (х1, х2.) = 2x1 2 4x1 + x2 - 3x2 2 линейна трансформация.

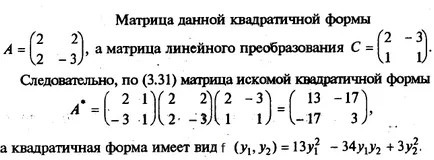
В квадратна форма, наречена каноничен (imeetkanonichesky изглед) ако цялата си koeffitsientyaij prii = 0 ≠ й, t.e.f (х1. X2. Xn) = a11 x1 + A22 х2 2 2 + ... + Ann Xn = 2.

Неговата матрица е диагонал.

Теорема (доказателството не е дадено тук). Всяка квадратна форма може да бъде намалено до каноничната форма като се използва не-линейна дегенеративен трансформация.

За да направите това, първо изберете точен квадрат на променливата x1:

Сега изберете точен квадрат на променливата x2:

Имайте предвид, че канонична форма на квадратна форма дефинира еднозначно (един и същ квадратното формата може да бъде намален до канонична форма различни начини 1). Въпреки това, получено по различни начини канонични форми имат редица общи свойства. По-специално, броят на термини с положителен (отрицателно) форма на квадратични коефициенти не зависи от метода на редукция за образуване на този вид (например, в примера винаги ще бъде два отрицателни и един положителен коефициент). Този имот nazyvayutzakonom инерцията на квадратните форми.

Трябва също да се отбележи, че рангът на квадратното форма се нарича ранг на квадратното форма. равен на броя на ненулевите канонична форма фактори и не се променя при линейни трансформации.

Квадратичен форма е (X) nazyvayutpolozhitelno (отрицателно) определен. ако за всички стойности на променливи не едновременно равни на нула, е положителен, t.e.f (X)> 0 (отрицателен t.e.f (X) <0).

Например, квадратна форма f1 (X) = x1 2 + x2 2 - положително определен защото представлява сумата от квадратите и квадратен formaf2 (X) = -Х1 2 х2 + 2х1 - х2 2 - отрицателен определен, защото е възможно да се представи videf2 (X) = - (х1 - х2) 2.

В повечето практически ситуации, да се установи категорично знак на квадратното форма е малко по-сложно, така че за тази цел един от следните теореми (ние ги изложи без доказателство).

Теорема. В квадратна форма е положителен (отрицателно) определено единствено и само ако всички свои собствени стойности са положителни матрица (отрицателно).

Теорема (критерий Sylvester). Квадратичната форма е положително определена единствено и само ако всички основни непълнолетните на тази форма са положителни.

Основната (ъгловата) второстепенен к-ти за матрица N-ия ред се нарича фактор на матрица, съставена от pervyhkstrok и колони от А () масив.

Имайте предвид, че за отрицателно квадратните форми се редуват определени признаци основните малолетни и непълнолетни лица, първият непълнолетния, за да е отрицателен.

Например, за да разгледа определен знак квадратна форма F (х1. X2) = 2x1 + 4x1 2 3x2 + x2 2.

Метод 1: Изграждане матрица квадратна форма А =. Характерните уравнението ще има формата = (2 -) * * (3 -) - 4 = (6 - 2- 3 +  2) - 4 =  2 - 5 + 2 = 0; D = 25 - 8 = 17. Следователно, квадратна форма - положително определена.

Метод 2. Мала основната първи порядък матрица А 1 = a11 = 2> 0. Основната малка втора poryadka2 = 6 - 2 = 4> 0. Следователно, критерий Sylvester квадратна форма - положително определени.

Проучване на друг определен знак квадратна форма, F = -2x1 + 4x1 2 х2 (х1, х2.) - 3x2 2.

Метод 1: Изграждане матрица квадратна форма А =. Характерните уравнението ще имат форма = (-2 -) * * (- 3 -) - 4 = (6 + 2 + 3 +  2) - 4 =  2 + 5 + 2 = 0; D = 25-8 = 17. Следователно, квадратна форма - отрицателен определен.

Метод 2. Мала основната първи порядък матрица А 1 = a11 = = -2 <0. Главный минор второго порядка2 = = 6 – 4 = 2> 0. Следователно критерий Sylvester квадратна форма - отрицателни определени (основни непълнолетни алтернативни признаци, вариращи от минус).

И като друг пример разглежда в определен знак квадратна форма F = 2x1 2 4x1 + x2 (х1, х2.) - 3x2 2.

Метод 1: Изграждане матрица квадратна форма А =. Характерните уравнението ще има формата = (2 -) * * (- 3 -) - 4 = (-6 - 2 + 3 +  2) - 4 =  2 + - 10 = 0; D = 1 + 40 = 41. Един от тези числа е отрицателен, а другият - положително. Признаци на собствени стойности различни. Вследствие на това квадратно формата може да бъде нито отрицателно, нито положително определена, т.е. Това квадратна форма не е определена (може да отнеме стойности на двата знака).

Метод 2. Мала основната първи порядък матрица А 1 = a11 = 2> 0. Основната малка втора poryadka2 = -6 - 4 = -10 <0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).

1Rassmotrenny метод за намаляване на квадратна форма на каноничната форма е полезна, когато има квадратите на променливи са ненулеви коефициенти. Ако не са, да извършва преобразуването все още е възможно, но трябва да използвате някои други методи. Например, Нека F (х1, х2.) = 2x1 х2 = x1 2 + х2 + х2 2x1 2x1 2 - х2 = 2