Координати и компоненти на вектора - решаването на проблемите на контрол

Координатна и векторни компоненти

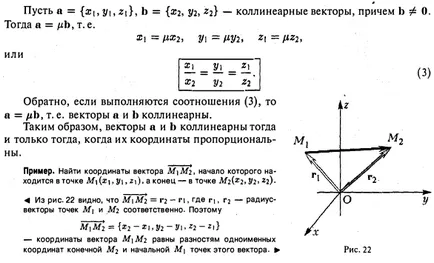
В правоъгълна Декартова координатна система пространство. Означаваме I, J, на единичен вектор (вектори) на положителни посоки на осите Ox. Oy, Оз (фиг. 19). Да разгледаме произволен вектор, началото на който е О, произход и коне - в точка А. Чрез точката равнина, перпендикулярна .osyam Ox, Oy и Оз. Тези плоскости се пресичат координатните оси в точките съответно Ру Q и R. Фиг. 20 показва, че вектори ОП, OQ, съответно, са колинеарни и ИЛИ единичен вектор I, J, K. обаче има числа х, у, 2, така че и следователно, координира и компонентите на формула (2) е вектор разлагане и възрастови / пори I, J, K. Тези методи всеки вектор може да бъде разложен на векторите I, J, к. Вектори, I, J, K са ортогонални и техните дължини са равни на един. Тройната I, J, K се нарича ортонормирана (координира) основа (ортонормирана база). Може да се покаже, че за всеки вектор разлагане и (2) въз основа на I, J, уникален, т. П. коефициенти. Y, Z в разлагането на вектора и векторите I, J, за еднозначно определени. Тези фактори се наричат ​​координатите на вектор. Те съвпадат с координатите х, Y, Z точка А - края на. Пишем в този случай Този пост означава, че свободният вектор уникално налага поръчаното тройна неговия произход. Векторите х \, т / й, ЗК, чийто размер е равен на вектора и се наричат ​​компоненти на вектор. От гореизложеното следва, че двата вектора и А = В = равно ако и само ако те са равни на координатите, т.е... Нека =, б = - колинеарни вектори, където В = 0. След това, L = TS, т.е. Координати и векторни компоненти Обратно, ако връзки (3), п = TS, т. Е. векторите А и В са колинеарни. По този начин, вектори, А и В са колинеарни ако и само ако техните координати са пропорционални. Пример. Виж координатите на вектора M \ Mi, началото на който е в точка М \ на (X \, г \, Z \). и в края - в точката Afi ( «2> 22). Фиг. 22, че M \ М = Т2 - п, където р. p2 - радиус вектори на точки M | и М, съответно. Затова - координатите на вектора М \ Mg, равни на разликите от подобен произход и заключителни MgO първоначална М \ точки на този вектор.