Като се има предвид броя на разпределение на дискретна случайна променлива вероятност да се намери изчезналите и за изграждане на

В случайна променлива X отнема само четири стойности: -4, -3, 1 и 2. Всяка от тези стойности е необходимо определена скорост. Тъй като сумата от всички вероятности трябва да е равно на 1, тогава вероятността липсва:

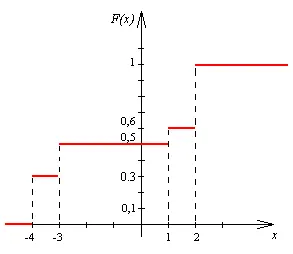
Ние образуват функцията за разпределение на случайна променлива X. Известно е, че функцията за разпределение, а след това:

когато, тъй като не стойност на х (-4, -3, 1 и 2) не е по-малко от х. това означава;

когато, тъй като само стойността -4 ще бъде по-малко от х. и събитието х = 1, се появява с вероятност, равна на 0.3, която е;

когато като стойности по-малки от х. ще бъде X = -4 и X = -3, и случайна променлива X може да приеме една първа или втора стойност, тогава;

Очакванията на дискретна случайна променлива е сумата на продукти от стойности на случайна променлива съответстващи на вероятността, т.е.

Дисперсия на дискретна случайна променлива намери формулата:

елементи на комбинаторика

Броят на комбинациите - - е броят на начините, по които можете да изберете, к отделни елементи от съществуващите наш елементи без да се отчита процедурата за вземане на проби.

Броят на разположения - - е броят на начините, по които можете да изберете, к отделни елементи от съществуващите наш елементи като се вземат предвид процедурата по вземане на проби.

Броят на пермутации - - е броят на начините, по които можете да изберете, п различни елементи от съществуващите наш елементи като се вземат предвид процедурата по вземане на проби.

Ето: - факториел

Действия по събития

Събитие - е само един факт, който може или не може да възникне в резултат на опит.

Комбинирането събития А и В - е събитие, което S. е вид или събитие или събитие Б. или двете събития в същото време.

Пресечната точка на събития А и В - е събитие, което е S. едновременно появата на двете събития.

Отричането на събитието - това е събитие, което не е появата на събитие А. Определяне на :.

Класическата дефиниция на вероятностите

Вероятността за събитие А - съотношението на броя на експериментите. благоприятна за възникване на събитие с общия брой на експерименти:

Вероятност умножение формула

Вероятност на събитието може да се намери от формулата:

- вероятност за събитие А,

- Вероятността за случай,

- Вероятността за дадено събитие, при условие че вече е настъпило събитие.

Ако събитията А и Б - са независими (появата на един не се отразява на външния вид на другия), а след това вероятността на събитието е:

Вероятност допълнение формула

Вероятност на събитието може да се намери от формулата:

- вероятност за събитие А,

- Вероятността за случай,

- вероятността от ко-възникване на събития А и Б.

Ако събитията А и Б - са взаимно изключващи се (не може да се появи по същото време), тогава вероятността на събитието е:

Общо вероятност формула

Нека събитието А може да се появи по същото време едно от събитията ... - нека ги наречем хипотези. Също известен - вероятността за удовлетворяване-тото хипотеза и - вероятността от събитие А, когато аз-ти хипотеза. След това вероятността за събитие А може да се намери от формулата:

Бернули схема

Нека жицата н независими проучвания. Вероятността за поява (успех) на събитие А във всяка от тях е постоянна и равна на стр. вероятност недостатъчност (т.е. няма поява на събитието A) р = 1 - стр. След това вероятността за к успехи в п проучвания могат да бъдат открити по формулата на Бернули:

Най-вероятният брой на успехи в Схема на Бернули - е броя на повторения на едно събитие, което съответства на най-високата вероятност. Може да се намери по формулата:

Случайни променливи

(Например, броят на момичетата в семейството с 5 деца) (например, време на правилната работа на чайника)

Числени характеристики на дискретни случайни величини

Нека дискретна стойност разположен в непосредствена близост разпределение: