Изграждане на графики на тригонометрични функции - Алгебра - 10 курсове за категории - резюмета на уроци
Tema.Postroenie графики на тригонометрични функции
Цел: Построяване функции у = грях х. у = COS х. у = TG х. у = CTG х.
Получаване на способности сюжетни функции: у = Asin (KX + б), у = Acos (KX + б), у = ATG (KX + б), у = ACTG (KX + Ь).
I. Проверка на домашна работа
1. Един от студентите играе решението за упражняване брой 24 (1-3).
2. Преден разговор:
1) Обадете явления в природата, които периодично се появяват отново.
2) Определяне на периодична функция.
3) Ако функция у = F (х) е броят на периода Т, периодът ще бъде функция от броя на 2T, 3 Т. А оправдае.
4) Да се намери най-малките положителни функции период:
а) у = COS; б) Y = грях; в) у = TG; щ) = у.
5) периодична функция у =? Ако отговорът е да, моля, посочете периода на функцията.
II. Изграждане на графиката на функция у = грях х
За конструиране на графиката на функция у = грях х използва единица кръг. Построява единична окръжност с радиус 1 см (2 клетки). Право изгради координатна система, както е показано на фиг. 57.
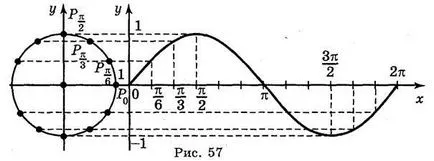
На оста х парцела на точките; π; ; 2 π (съответно 3 клетки, 6 клетки 9 клетки 12 клетки). Раздел на първото тримесечие на единичната окръжност на три равни части и същия брой парчета нарязани на оста х. Прехвърлете задължително стойност на съответния точки ОХ ос. Качваме се на мястото, което трябва да бъде свързан с гладка линия. След разделяне на втората, третата и четвъртата четвърт на единица окръжността, на три равни части и да прехвърли стойността на синуса на съответната точка оста х. Последователно комбиниране на всички точки на данни, ние получаваме графиката на функция у = грях х в интервала [0; π].
За причината, че функция у = греха х периодична с период от 2 π. е да се парцел х функция у = грях на цялата линия ОХ успоредна достатъчно, за да се движат изобразени по оста х от 2 π. 4 π. 6 π. дяловете си наляво и надясно (фиг. 58).
Крива, която е графика на х функция у = грях. наречен синусоида.
1. Конструкция графиките на функции.
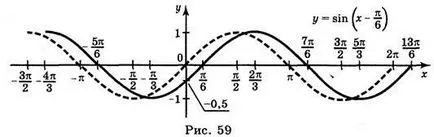
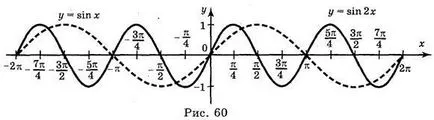
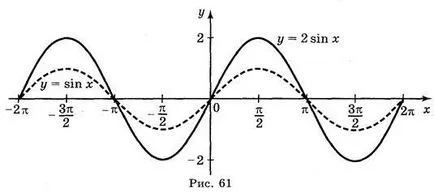
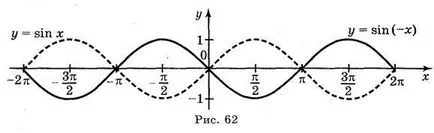
а) Y = грях; б) = грях Y 2; в) Y = грях 2 х; г) Y = грях (-x).
Отговори: а) Фиг. 59; б) Фиг. 60; в) Фиг. 61; г) Фиг. 62.
III. Изграждане на графиката на функция у = COS х
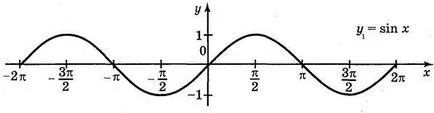
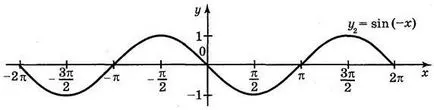
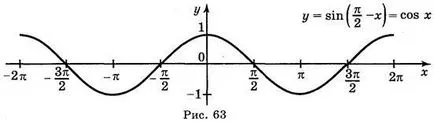
Както знаете, COS х = грях. така = COS х и у = грях - същата функция. За конструиране на графиката на функция у = грях употреба геометрични трансформации на графики: първо конструират (Фигура 63) Графиката на у = грях х.. тогава Y = грях (-x) и завършва в = грях.
1. Начертайте графиките на функциите:
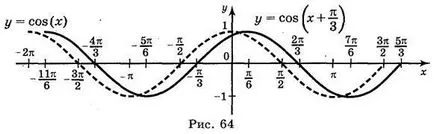
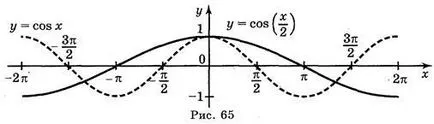
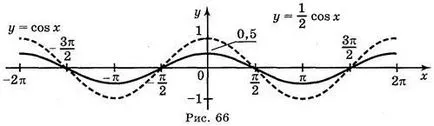
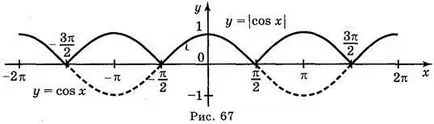
а) у = COS; б) у = COS; а) у = COS х; г) = у | COS х |.
Отговор: а) Фиг. 64; б) Фиг. 65; в) Фиг. 66; г) Фиг. 67.
IV. Изграждане на графиката на функция у = TG х
Графиката на функция у = TG х конструира чрез допирателната линия на интервал, чиято дължина е равна на π период на тази функция. Построява единична окръжност с радиус 2 см (4 клетки) и се направи линия допирателна. Право изгради координатна система, както е показано на фиг. 68.
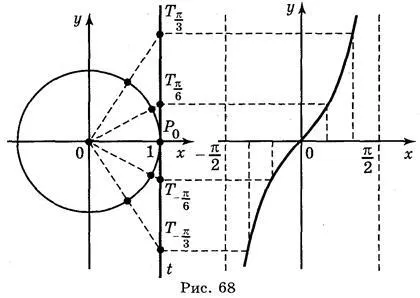
На оста х парцела на точките; (6 клетки). Разделете първо и четвърто тримесечие кръга на 3 равни части и на същите части, и всеки от сегментите. Нека да се намери стойността на допирателната на номера; ; 0; ; през линия допирателна (съгласува точки ;;;; допирателна линия). Трансфер на стойностите на съответните точки на допирателните ОХ ос. Последователно се събират всички точки на данни, ние се графиката на у = TG х в интервала.
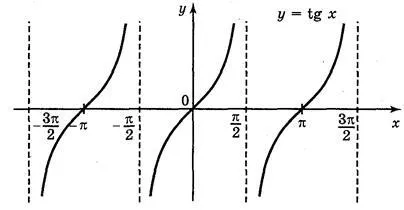
За това, че у = функция TG х е периодична с период π да парцел ш функция = TG х на цялата линия ОХ успоредна достатъчно, за да се движат изобразени по оста х в π. 2 π. 3 π. 4 π. единици от ляво и в дясно (фиг. 69).
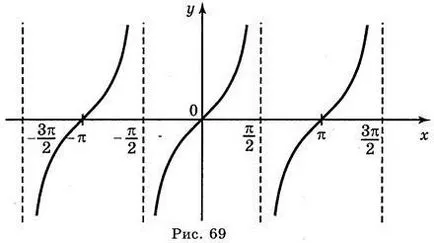
Графиката на у = TG х tangensoїdoyu наречен.
1. Графика функции
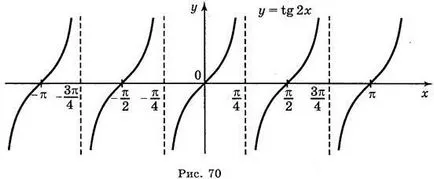
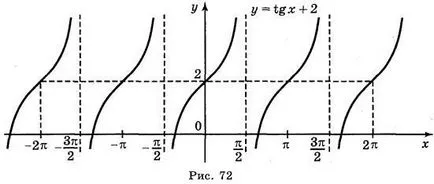
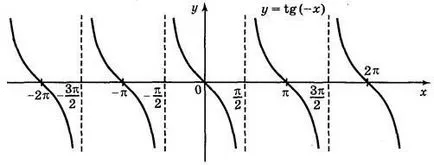
а) в TG = 2; б) у = т г х; в) Y = TG х + 2; г) Y = TG (-x).
Отговори: а) Фиг. 70; б) Фиг. 71; в) Фиг. 72; г) Фиг. 73.

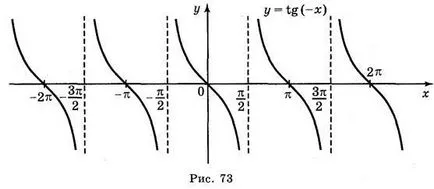
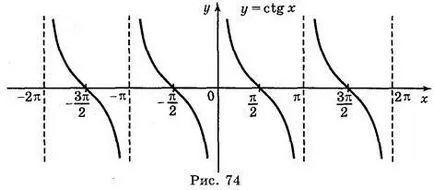
В. Конструиране на графиката на функция у = CTG х
Графиката на функция у = CTG х лесно получава при използване на формула CTG х = TG и два геометрични трансформации (фиг. 74) по отношение на оста на симетрия ΟΥ паралелно транслация по оста х.
IV. домашна работа
Раздел и § 6. Въпроси и задачи за раздел повторение и номер 50-51. Речник № 28 (A-D).