Интересни проблеми с практическо съдържание

1. Повторението Теория

а) Сходство на триъгълници.
б) Пропорционално сегменти в кръга.

2. думите на Учителя за целите на този урок

Геометрия - това не е само наука за триъгълници свойства, успоредник, кръгове. Геометрия - е цял един свят, който ни заобикаля от раждането. След всичко, което виждаме около нас, един или друг начин свързани с геометрията, нищо избягва внимателен й поглед. Геометрия помага на човек да преминете през света с широко отворени очи, да научите внимателно огледайте и вижте красотата на обикновените неща, да гледате и мисля, мисля, че и правят заключения.

В урока ще обсъдим интересни задачи за решаване, които ще помогнат на знанията на геометрията, че студентите имат в 8-ми клас.

3. Представяне на един от студентите с кратко съобщение за Конан Дойл

Световноизвестният писател Артър Конан Дойл е бил лекар.
Но той е много добър, най-вероятно е знаел геометрия. В историята "Ритуалът на рода Мъсгрейв" той определи като Шерлок Холмс трябваше да се определи къде края ще бъде в сянката на дървото, бряст, който се намали. Той знаеше, че височината на дървото по-рано. Шерлок Холмс обясни действията си: "... Аз свързан с две пръчки, които ми дадоха шест крака, а аз и моят клиент отиде на мястото, където той веднъж нарасна бряст. Подадох прът в земята, каза посоката на сянка и да го измери. Беше девет фута.
Освен това моите изчисления са наистина доста лесно. Ако пръчката е висок шест фута хвърля сянка на девет фута, височината на дървото на шестдесет и четири крака хвърля сянка в деветдесет и шест крака, а по посока на една или друга страна, разбира се, ще бъде същото. "

Задача 1. Измерване на височината дърво

За да се измери височината на дърво BD се получава АВ1 С1-правоъгълен триъгълник с ъгъл А = 45 и го държи вертикално, се премества на разстоянието, на което, гледайки по АВ1 хипотенузата. видя на върха на Р. дърво Каква е височината на дървото, ако разстоянието
AC = 5,6m и височина 1,7 м на лицето?

1), тъй като е обща за двете триъгълници, и АС1 В1 и DIA (от хипотеза) директно (т.е., равно на 90), на АС1 В1 и DIA - като (на базата на сходство на 2 ъглите).
2) След това АВ1 С1 = ABC = 45 о. => BC = AC = 5,6m, но за да получите дължината, ние трябва да се прибави височината, т.е. дължината на дърво DB = 7,3m.

Задача 2. кула враг

Open пътна отсечка, съхранявани на лента с ширина 50 метра AB; враг наблюдателен пост на се намира в горната част на височина камбанария MN = 22м. Какво трябва да направи височина вертикално HF маска на разстояние 500 метра от камбанарията да затвори пътя от наблюдателя на врага?

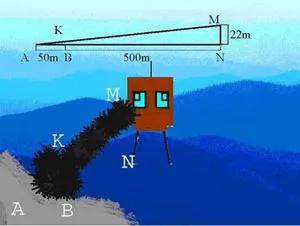
AMN, AB = 50 m,
MN = 22 метра,
BN = 500 метър

AMN (2-ри ъгли: A - Най-общо, AVK и AMN - прави, и ако триъгълници са подобни, тогава всичките му елементи, също са като думи, и по тази причина, м ...

Цел 3. Land с един поглед, когато сте в небето с балон

Колко далеч може да се види от балон, който се е повишила до височината на 4 км над Земята (приблизително равно на 6370 km радиус на Земята)?

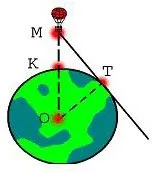
1. Чрез теоремата на допирателната към окръжността, перпендикулярна на допирателната на радиус провежда до точката на контакт, т.е. OTM = 90.
2. MO = 4 + 6370 = 6374 km,
3. Тогава питагорова теорема:

MT 2 2 + OT = MO 2
MT 2 = МО 2 - OT 2

MT = 112,9 км

Задача 4. Определяне на разстоянието от корабите в морето

Адрес на специфични практически проблеми на старата може да намери приложение в настоящето, и затова заслужават внимание.
История на геометрия държи много за решаване на проблеми техники, за да се намери разстоянието. Определяне на разстоянията до корабите в морето, - една от тези задачи, за да бъде решен по два начина.
Намерете разстоянието от точка А разположен на брега до кораба

1-ви начин. Нека корабът е в точка К, както и на наблюдателя в точка А е необходимо да се определи разстоянието на космическия кораб. Чрез изграждането на прав ъгъл точка А, е необходимо да се отложи до брега две равни сегменти AB = BC. В буква отново се изгради под прав ъгъл, наблюдателят трябва да следва перпендикуляра нагоре, докато стигне до точка D, от която превозното средство К и точка Б ще се види, да лежат на една права линия. правоъгълен триъгълник VSD и ВАК са, следователно, CD = AK и CD участък може да се измерва директно.

Вторият метод. наречен метод триангулация. Намерих приложение в астрономията. С помощта на измерените разстояния до небесни тела. Този метод се състои от 3 етапа:

1. Измерване на ъгли 1 и 2, и разстоянието AB.
2. Изграждане A'V'K "с ъгли 1 и 2 във върховете А 'и В', съответно.
3. Като се има предвид сходството на триъгълници ABK, A'V'K "и равенство, известната дължина на сегмента AB, * за" "и" Б "не е трудно да се намери един сегмент с дължина на АК.

Поет Г. Лонгфелоу е и математик. Може би затова най-ярки изображения, които красят математически понятия, които той използва в романа си "Кавана", улавя някои от най-теореми и тяхното прилагане. Четем следната задача в роман Лонгфелоу е:

"Лили, един инч, се издига над повърхността на водата, а порив на вятъра свеж докосна повърхността на езеро в лактите на двама бивши място: на тази основа да се определи необходимата дълбочина на езерото." (1 инч равно на 10 инча, две лакът 21 инча)

И този проблем е решен въз основа на теоремата: Ако две хорди се пресичат в кръг, а след това на продукта от дължините на части от един от тях е равна на произведението от дължините на другите части.
Вижте снимката, и след като става ясно, тъй като дълбочината на езерото е (х):

Отговор: 17.05 инча.

В урок бяха обсъдени най-належащите проблеми, свързани с геометрични измервания на земята - определянето на височината на обекта, намери разстоянието до недостъпни обекти. Тези цели са от значителен практически интерес, засилване на знанията, придобити в геометрията и може да се използва за практическа работа. Ценна е, че техните решения не се нуждаят от познания повече в сравнение с размера на 8 класове.

Елбрус (Кавказ) се издига над морското равнище до 5600 m. Колко далеч може да се види от върха на тази планина?

М - наблюдение след височина Н метра един над земята; Земята радиус R, MT = г е най-големият видимо разстояние. Докажете, че.

Намерете разстоянието от острова, разположен на брега на езерото, до точка Б по крайбрежието. (На острова, за да поеме точка).

Най-горе в планината може да се види от точка А под ъгъл от 38 # 01; 42 ', както и подходът към планината до върха на 200 метра се виждаше под ъгъл от 42 # 01;. Намерете височината на планината.

1. Sergeev ПО Olekhnik SN Gashkov SB "Прилагане на математиката", Wiley Science 1989 година.

2. насипни MB Болк GD "Математика след училище" М. Образование 1971.

3. Chetverukhin NF "Методи на геометрични конструкции", М. Uchpedgiz 1952.

4. Kosyakin AS Никулин AS Смирнов AS "Управление на земя", М. Nedra 1988 година.

6. AV Tkachev Начало математика 8 клас

8. Ако Sharygin Erganzhieva LN Visual геометрия.