Инерционни моменти
Оттук част от областта се намира в квадранта I и III, имат положителен центробежен инерционен момент, като продукт на координатите х и у елементарни области DF, като в тези квадранти има положителни стойности. Част от областта намира в квадранта II и IV има отрицателни центробежни инерционни моменти.
Моментите на инерция около оси, успоредни, една от които е централно (XC0CYC) depyayutsya дефинирани от изрази (фигура 4.7.):
където А и В - разрез център на тежестта координира ° С
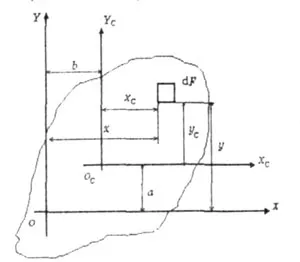
Координати а и б трябва да бъдат заместени в тези формули по отношение на техните признаци.
В моменти на инерция, влизащи във формулата за определяне на силата и твърдостта са изчислени за оси, които не са само централната, но и от първостепенно значение. За да се определи кои ос, минаваща през центъра на тежестта са основните, е необходимо да бъде в състояние да определи моменти на инерция около оси завърта спрямо друга от определен ъгъл.
(. Фигура 4.8) зависимости между моментите на инерция по време на въртенето на координатните оси имат формата:
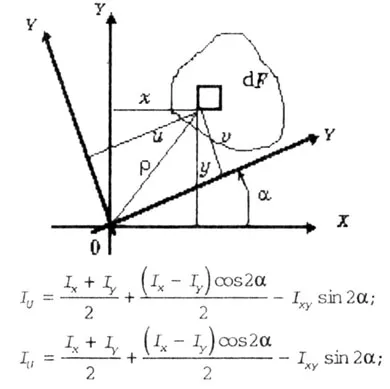
където - ъгълът между осите и XOY UOY. Ъгълът е положителен, ако XOY оси на въртене на часовниковата стрелка.
Основните оси на инерция се наричат две взаимно перпендикулярни оси, за които центробежната момента на площ е нула.
Посоката на главните оси на инерция, определен от уравнението
Основни инерционни моменти се наричат осови инерционни моменти, изчислени по отношение на основните оси на инерцията, които са на екстремните стойности на
Основната ос, минаваща през центъра на тежестта на секцията, наречена главните централни оси. и моментите на инерцията за тези оси са основните централни инерционни моменти.
Оста на симетрия на плосък участък е | главната централна ос на инерция на секцията.
Ако секцията равнина има поне две оси на симетрия на не-перпендикулярни една на друга, всички оси, минаващи през центъра на тежестта на фигурата, са централните главните оси на инерция. аксиални сечение моменти на инерция, изчислени по отношение на тези оси равни една на друга (фиг. 4.9).