Физически и Математически общество в гимназията - с решаването на проблема

Проблеми с решението. Трептения и вълни

1) върху гладка хоризонтална натоварване е свързан чрез пружина към стена. Честотата на природните осцилации ω. Cargo бе отстранен от позицията на равновесие в дясно в л и освободен. След отклонение време от равновесното положение на товара достига л / 2. Каква е неговата скорост в момента. когато ускорение е грама.

1) заместване на първоначалните условия

2) Изразът за ускоряване на колебание е:

Тъй като предположение. а = грам. на

За скоростта имаме:

2) Kubik осцилира с период от една секунда във вертикална равнина на сферична чаша, вътрешния радиус на което е много по-голяма от ръба на куб. Bowl в покой спрямо Земята. Какво ускорение спрямо земята и в каква посока трябва да се движи вертикално купа да умре за време 1,5 мин 60 прави трептене.
Решение.
Колебанията куб еквивалентни трептения математическо махало. В действителност, след като движението на куба върху вътрешната повърхност на сферичната купата става без триене колебанията на куба, на ръба на който е много по-малки от радиуса на чашата може да бъде заменен от колебанията на тялото, геометричните размери, които са много по-малки от дължината на нишката, на която виси, точката на окачване е в геометричния център сферична купа, и дължината на преждата, равен на радиуса на купата.

Според проблема, докато чашата почива спрямо Земята, за периода на трептене T 0 е куб. сила на опъване на конеца съобщава в кубичен равновесие ускорение равно модул ускорение на свободно падане, и насочена вертикално нагоре. след това

където R - дължина нишка, равен на радиуса на сферичната повърхност на чашата.

Когато вертикално ускорение спрямо земекопна прежди напрежение силите на споменатата чашка кубичен състояние на равновесие ускорение г ± а. където знака плюс съответства на ускорение насочена нагоре, и знак минус - ускорение насочена надолу. Да предположим, че за определеност

От изрази (1) и (2) намираме отношението на периодите:

Анализ показва резултата от решаването на проблема, че посоката на вертикално движение на купата (т.е. по посока на неговата скорост) не е засегната в периода на трептене на куба. Важно е да се знае посоката на ускорението.

В този случай, ускоряване на посока надолу на купата, и е възможно или в ускорено намаляване на купата или по време бавно се увеличава. Модул същото ускорение е

3) поплавъка Течният плътност ρzh височина цилиндър часа. Ако бутилката е потопен дълбоко в течността, или алтернативно, издърпайте малко на течността, след като е бил освободен, цилиндърът започва да се люлее. Плътността на материала, от който е направен на цилиндъра, ρm. Определяне на честотата на трептене на цилиндъра.

Състоянието на тялото на плуване: силата на Архимед, равна на силата на тежестта:

където S - площта на напречното сечение на цилиндъра, х 0 - дълбочина на потапяне.

Ние определяме дълбочината на потапяне на цилиндъра:

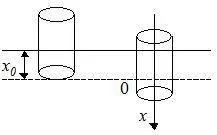
Ако увеличите дълбочината на потапяне на цилиндъра, силата на тежестта няма да се компенсира за плавателност и основен закон на динамиката на цилиндъра (в проекцията на посоката на оста х. Заедно, които се срещат на вибрациите) ще изглежда така

където х - изместване на цилиндър спрямо положението на равновесие, или

Ускорение хармонични трептения варира съгласно формулата. Сравнение с (1), до получаване на естествената честота на трептене

4) е колона дължина L на течност в образната тръба U. За кратки промени течност под налягане в коляното течни нива изместен и колоната започва да се колебае. За да се определи честотата на трептене. Стена триене пренебрегвани.

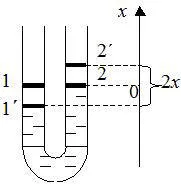
Чрез преместването бара на х в повишенията на правилното ниво на коляното от х. и в ляво пада -x (несвиваем флуид) на. Fluid движение ще се появи по време на действието на силите на налягането:

където S - зоната на тръбата, Р напречно сечение - налягане.

Според втория закон на Нютон

където m - маса на течност. знак минус се приема, защото силата на натиск е насочен в посока, обратна на изместване. Ето защо,

Сравнение с формула за ускорение. Ние получи за ω

5) Към свободно окачена пружина скованост на приложеното натоварване тегло М и освободен. Трептенията умират бавно. Намери: 1) от максималната деформация на пружината; 2) енергия вграден в тялото, след като прекратят вибрациите напълно.
решение:
Позицията на равновесие на тегло М през пролетта ще бъде по-ниска от x0 първоначалната позиция на масата :. Тъй като вибрациите се погасява бавно в първото натоварване половин цикъл падне под x0 равновесното положение също почти (началната амплитуда). С други думи, максималната деформация на пролетта ще бъде
.
Енергийна вграден в тялото, ние откриваме, закона за запазване на енергията. В първоначалното състояние на натоварването на системата има потенциална енергия. Тази енергия (крайно състояние) е преместен в енергия на пружинната деформация и топлина Q:

Оттогава

1,443,955 уникални посещения