Етаж и ICU степен и Радиан мярка на ъгъла

Градиент usnaya Ная и радиан измерване на ъгъл. тригонометрични кръг

Ако ъгълът α ° и включва едновременно измерени х радиани. след това. където К ° - постоянен коефициент. Заместването, например, и. Ние получаваме. На противно ,. къде.

Пример 1. изразяват в радиани солна най ъгли от 90 °, 45 °, 60 ° и 27 °.

Решение. И с формула (2) :.

Пример 2. Експресират поне ° С usnoy ъглите в радиани.

Решение. И с формула (2) :.

Ротация около точката на произход

Помислете кръг на координатната равнина радвам iusa 1 центрирана в произхода. Тя се нарича единичната окръжност. Ние въведе понятието повратната точка на единица кръг по отношение на произхода на ъгъл на а радиани. където α - всяко реално число.

1. 1. Нека α> 0. Да предположим, че една точка подвижна poedinichnoy обиколка от точка Р на часовниковата стрелка преминал дължина на пътя α (фиг. 1). Крайна точка на пътя обозначен с М.

В този случай се каже, че точка М се получава от P чрез завъртане около произхода на ъгъл на а радиани.

2. 2. Нека α <0. В этом случае поворот на угол α радиан означает, что движение совершалось по часовой стрелке и точка прошла путь длинной (рис. 2).

Завъртане на 0 Рад означава, че точката остава на място.

1) Когато повратна точка Р (1 ;. 0) под ъгъл (фигура 3) се получава от М точка с координатите (0, 1).

2) Когато повратна точка Р (1 ;. 0) под ъгъл (фигура 3) се получава точка N (0, 1).

3) Когато повратна точка Р (1 ;. 0) под ъгъл (фигура 4) се превръща в точка R (0, 1).

4) С повратна точка Р (1 ;. 0) под ъгъл (фигура 4) се получава от точка А (1; 0).

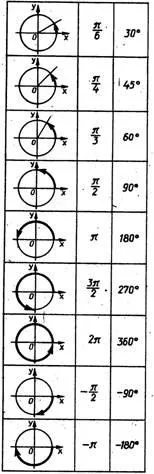
Тук маса ротации в някои ъгли, изразени в радиани и солна стъпки ° С usnoy (фиг. 5).

Имайте предвид, че при завъртане на точка Р (1, 0) в 2, т.е. 360 °, въпросът се връща в първоначалното си положение (вж. Таблицата). При включване на точка -2, т.е. при -360 °, той също се връща в първоначалното си положение.

Да разгледаме точка примери завъртане под ъгъл по-голям от 2 . и ъгъл по-малък от -2 . Така че, когато включите точка ъгъла изпълнява два пълни оборота обратно на часовниковата стрелка и минава по друг път (фиг. 6). При включване на точка в корнер прави два пълни оборота по часовниковата стрелка и друг път се простира в същата посока (фиг. 7).