Експоненциален уравнения и неравенства

Мнозинство решение на математически проблеми в един или друг начин свързани с превръщането на цифровата, алгебрични или функционални изрази начин. Горното се отнася особено за решението на експоненциални уравнения и неравенства. В изпълнения ИЗПОЛЗВАТ математически проблеми за този тип включват, по-специално, С3 задача. Научете как да се реши задачата C3 е важно не само да преминат успешно изпита, но и поради причината, че това умение е полезен при изучаването на математика в гимназията.

Преди да се пристъпи към анализ на специфични експоненциални уравнения и неравенства. като преподавател по математика, предлагам ви да реша на някои от теоретичния материал, който ни трябва.

експоненциална функция

Какво е експоненциална функция?

Функция на форма у = а х. където> 0 и ≠ 1, се нарича експоненциална функция.

Основните свойства на експоненциален funktsiiy = а х:

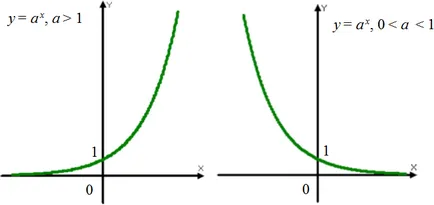
Графики на експоненциална функция (експоненциална)

Решение на експоненциални уравнения

Примерна са уравнения, в които неизвестен променлива е само по отношение на който и да е степен.

За решаването на експоненциални уравнения трябва да знаят и да могат да използват следната проста теорема:

Освен това, е полезно да се помни, за основните формули и действия с градуса:

Пример 1. решаване на уравнението:

Решение: С помощта на горната формула и заместването:

Уравнението тогава става:

В дискриминантата на квадратното уравнение, получен е положителен:

Това означава, че уравнението има две корени. Намерете ги:

Що се отнася до обрат в замяна получаваме:

Второто уравнение още няма корени, тъй като експоненциална функция е строго положително върху целия домейн. Решете втората:

С това каза, в Теорема 1 пропуск за еквивалентно уравнение: х = 3. Това би било в отговор на тази работа.

Пример 2: решаване на уравнение:

Решение: ограничения върху обхвата на допустимите стойности за уравнението са, както радикал експресия има смисъл за всяка стойност на х (експоненциална функция Y = -x 09 април е положително и не е нула).

Решаването на уравнение с помощта на еквивалентни правила трансформация умножение и деление степени:

Последният преходът се извършва в съответствие с Теорема 1.

Пример 3: решаване на уравнение:

Решение: от двете страни на първоначалното уравнение може да бъде разделен на 0,2 х. Този преход би означавало, както този израз е по-голяма от нула, за всяка стойност на х (експоненциална функция е строго положително на потребителите). Тогава уравнението е:

Пример 4. решаване на уравнението:

Решението: опрости уравнението до елементарна чрез еквивалентни преобразувания прилагане на понижени в самото начало на правилата за разделение и умножение на степени:

Разделяне двете страни на уравнението от 4 х. Както и в предишния пример, това е еквивалентно на трансформация, тъй като експресията не е равна на нула за всяка стойност на х.

Пример 5 решаване на уравнението:

Решение: функция у = 3 х. лявата страна на уравнението, се увеличава. у функция = -x -2/3, дясната страна на уравнение намалява. Това означава, че ако графиките на тези функции се припокриват, а след не повече от една точка. В този случай, не е трудно да предполагам, че графиките се пресичат в точка х = 1. Други корени няма.

Пример 6. решаване на уравнението:

Решението: опрости уравнението чрез еквивалентни преобразувания, като се има предвид, че винаги експоненциалната функция е строго по-голямо от нула за всички стойности на х и с помощта на правилата за изчисляване на продукта и отношението на градуса, дадени в началото на статията:

Решение демонстрация на неравенството

Примерна нарича неравенство, в които неизвестен променлива се съдържа само в изпълнението на всички сили.

За решаването на експоненциални неравенства изисква познаване на следната теорема:

Пример 7. решаване неравенство:

Решение: Да приемем първоначалната неравенството във формата:

Разделете двете страни на това неравенство с 3 2x. в същото време (поради позитивност на функция у = 3 2х) знак неравенство няма да се промени:

Тогава неравенството става:

Така, разтворът на разликата неравенството е:

преминаване да се обърне на заместването, получаваме:

Левият неравенство се дължи на позитивност на експоненциалната функция се извършва автоматично. С помощта на познатите свойства на логаритъм, се минава към еквивалент неравенството:

Тъй като основа на степента е число по-голямо от един еквивалент (теорема 2) ще се премести на следното неравенство:

Така че, ние най-накрая да получите отговор:

Пример 8. решаване неравенство:

Решение: С помощта на свойствата на умножение и деление на властите, ние пренапише неравенството като:

Въвеждаме нова променлива:

С оглед на това неравенство заместване става:

Ние умножим числителя и знаменателя със 7, получаваме следния еквивалент неравенството:

Така че неравенството отговарят на следните стойности на променлива Т:

След това се обърна към обратната замяна получаваме:

Тъй като основата на мощност е по-голямо от едно, това е еквивалентно на (от теорема 2) ще се премести в неравенството:

Най-накрая да получите отговор:

Пример 9. решаване неравенство:

Разделете двете страни на неравенство в израза:

Винаги е по-голяма от нула (поради позитивното на експоненциалната функция), така че няма нужда да се промени знака на неравенството. получаваме:

Ние използваме промяната на променлива:

Оригиналният уравнението тогава става:

Така че неравенството задоволи стойности на тон. разположен в пространството:

Що се отнася до замяната назад ние откриваме, че първоначалното неравенство е разделен на два случая:

Първото решение на неравенството не се дължи на позитивното на експоненциалната функция. Решете втората:

Тъй като основата на мощност в този случай е по-малко от един, но по-голяма от нула, което се равнява на (теорема 2) ще се премести на следното неравенство:

Така че, окончателен отговор:

Пример 10. Определете неравенство:

Клоновете на у парабола = 2х + 2x 2, насочени надолу, поради което се ограничава горе от стойността, която достига в своя връх:

Клоновете на парабола Y = х 2 -2x 2, стояща на експонентата са насочени нагоре, така че да се ограничава до под стойността, която достига своя връх:

Заедно с това е ограничена по-долу и функция у = 3 х 2 -2x 2. от дясната страна на уравнението. Той достигна най-ниската си стойност от същото място като парабола стои в индекса, а стойността е 3 1 = 3. Следователно, първоначалната неравенство може да е вярно, само ако това е функция на лявата и дясната приемате по едно и също точка стойност равно на 3 (пресечната точка на диапазоните на тези функции е просто число). Това условие е изпълнено в една точка х = 1.

За да научите за решаване на експоненциални уравнения и неравенства, трябва постоянно да се обучават в решението им. В този труден въпрос, за да можете да помогнете на различни наръчници, книги, посветени на проблемните елементарна математика, колекции от конкурентни задачи, курсове по математика в училище, както и индивидуални сесии с професионален треньор. Искрено ви пожелавам успех в подготовката и отлични резултати в изпита.