Докажете Питагоровата тригонометрични самоличността

Питагоровата тригонометрични идентичност е по следната формула:

sin2 α + cos2 α = 1

Това означава, че в правоъгълен триъгълник сборът от квадратите на синуса и косинуса от същия остър ъгъл е равен на единица.

Нека да докажат това тригонометрични идентичност. При един правоъгълен триъгълник ABC (∠C = 90º). Ние го привлече към височината на хипотенуза гл.

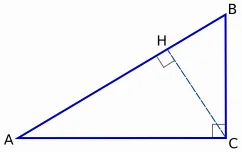
Ние изразяваме краката на триъгълника ABC на уют. Тъй като COS А = AC / AB, тогава

Тъй като COS В = BC / AB, на

А сега да разгледаме триъгълника АСН. Той е прав, т. За. CH ⊥ AB. Тъй като в този триъгълник е хипотенузата. Тогава защото A = AH / AC. Ние изразяваме тук сегмент AH:

Ние замени сегмент AC своята стойност, изразена по-рано от косинус на ъгъла А ABC триъгълник. получаваме:

AH = (AB · защото А) · COS А = AB · защото 2 А

А сега да разгледаме триъгълника BCH. Това COS В = BH / BC. Ние изразяваме BH BC и да се замени стойността си намери в триъгълник ABC:

BH = AB · защото 2 B

Дължината на AB е сумата от дължините AH и БХ:

Сменете AH и BH по израженията им от гледна точка на косинуси:

AB · защото 2 + AB · защото 2 B = AB
AB · (COS 2 + 2 защото B) = AB
COS 2 A + защото 2 B = 1

Както е известно, правоъгълен триъгълник е равен на косинус на острия ъгъл на друг от същия триъгълник синуса на остър ъгъл. В този случай:

Следователно, в идентичността защото A + защото 2 2 B = 1, може да се замени косинуса на ъгъла В на синуса на ъгъла А. Така получаваме:

COS 2 A + защото 2 B = 1
COS 2 + (COS B · защото B) = 1
COS 2 + (син А · грях А) = 1
2 защото 2 + грях А = 1

Така, сумата от квадрата на косинуса на ъгъла и квадрата на синуса на ъгъла е равна на единица, както се изисква.