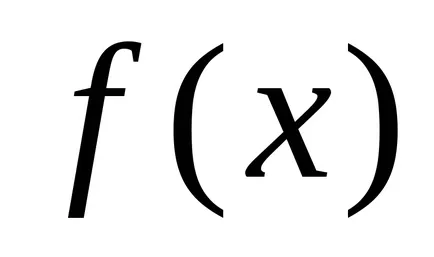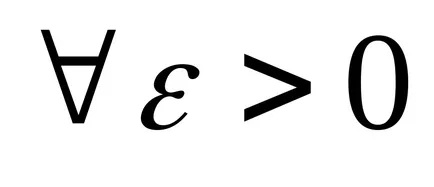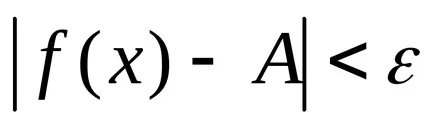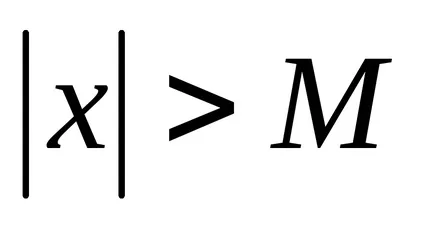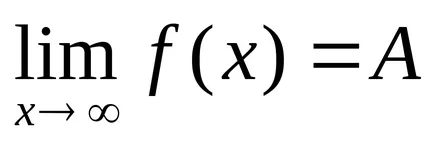числова поредица
Помислете за множеството на естествените числа 1, 2, 3, 4, ... ..n, ...
Нека всеки естествено число според някои правило или закон се възлага на реално число x1. x2. x3. ... хп. ... Тогава ние казваме, че множеството на естествените числа се дава числен последователност п>.
Числовата последователност е определен, ако от които може да се изчисли всеки член на последователността, посочена правило, освен ако не е известен брой. Това правило се нарича formuloynchlena последователност.
Например: х 2 = N
сходяща редица
номер се нарича границата на п последователности>, ако за всяка д> 0 има chisloN (ε), така че за vsehn> nYou неравенство │hp - a│<ε. Обозначают
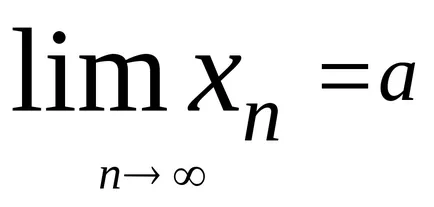
Последователност с граница се нарича конвергентна.
Неравенството │hn -a│<ε равносильно неравенству а – ε <хn номер се нарича граница на последователността, ако по някаква електронна> 0 съществува chisloN (ε), че всички условия за последователността с nomeramin> Npopadut в епсилон - квартал на. Извън този квартал има или няма хп точки. или има определен брой от тях. Теорема 1. Ако последователността има ограничение, то е уникално. Нека последователността има две различни лимит и а и б. Помислете квартал на точки ibtakoy малки количества, че те не се пресичат. Ние използваме втория последващо определяне граница-последователни. От броя и последователността на границата, тогава съществува точка квартал и че всички членове, с изключение на поредицата могат да бъдат от краен брой попадат в ε - квартал на. Тъй като лимит chislobyavlyaetsya на последователност, всички от гледна точка на последователността, с изключение на само определен брой от тях попадат в ε - tochkib квартал. По този начин, всички членове на снимачната площадка са безкрайни в околностите на две различни точки, които не могат да бъдат. Противоречие. Следователно, само на лимита, и теоремата е вярно. Якост алгебрична сума от краен брой последователности е равна на сумата от алгебрични отношение на последователности извън ако съществуват последните граници. Граница на продукт на краен брой последователности е равна на произведението на факторите на последователности извън ако съществуват последните граници. Ограничаване частни последователности е самостоятелна извън числителя и знаменателя, ако съществуват тези граници и границата на знаменателя на последователност е различна от нула.Основни свойства на граници
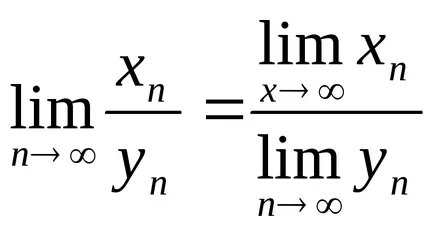
Нека докажем, например, първото твърдение.
Да предположим, че има две последователности от п> и п> и сумата от п + ин>. За да се докаже, че
Ние използваме дефиницията на граница последователност.
нека
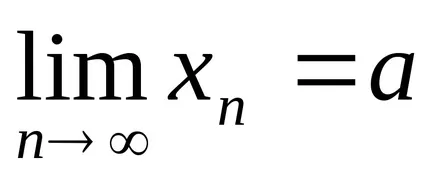
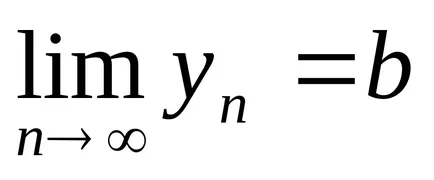
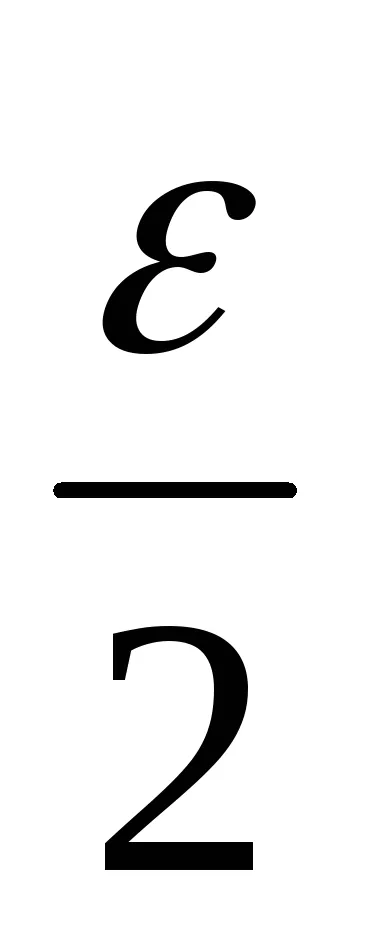
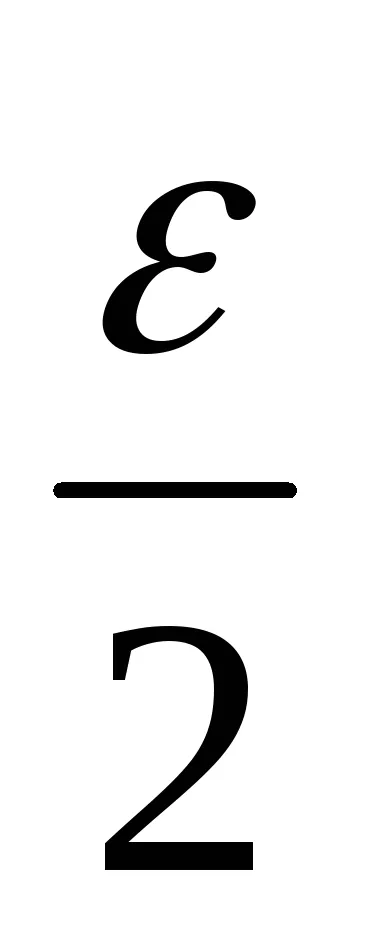
Форма на модула на разликата между броя последователност на сума и nchlenom (А + В) и го използва за свойствата на модула и горните неравенства.
│ (хп-ин) - (А + В) │ = │ (хп -а) + (Ь ин) │<│xn -a│+│yn -b│<
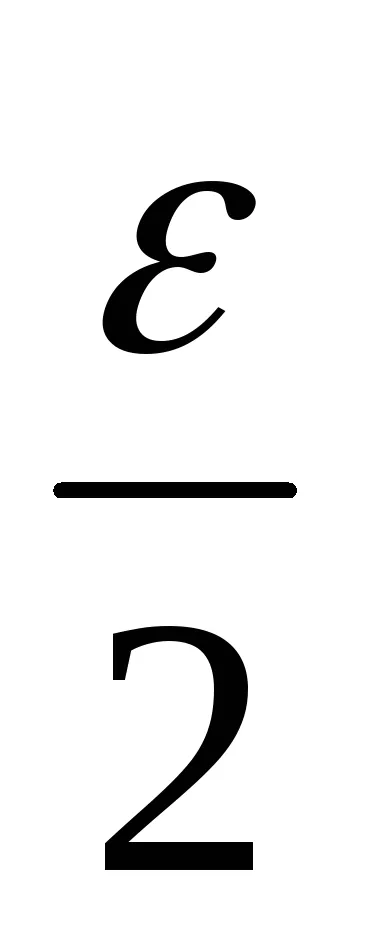
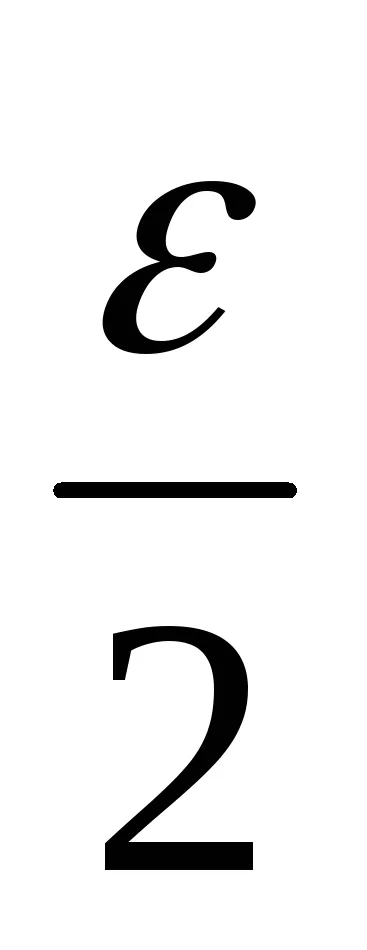
След това, от граница определение последователност, изявлението в рамките на поредица точното количество на.
Останалите твърдения се оказаха по подобен начин.
Нека функцията
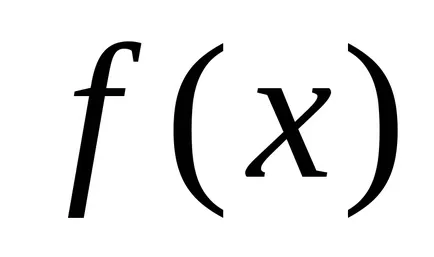
Определение 1. Броят А се нарича граница на функцията
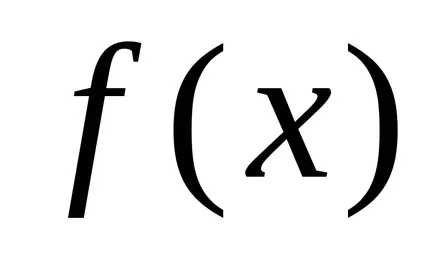
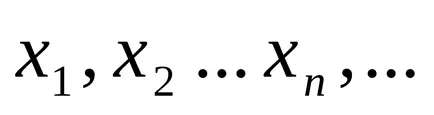
Обърнете се към него по този начин:
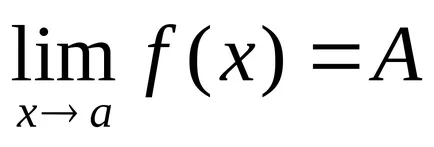
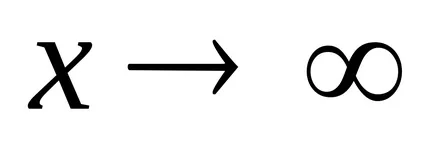
Ако последователността на стойности на функцията тенденция да
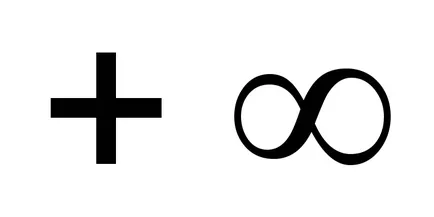

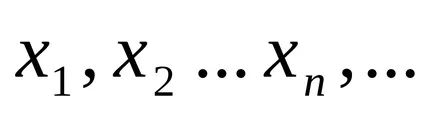
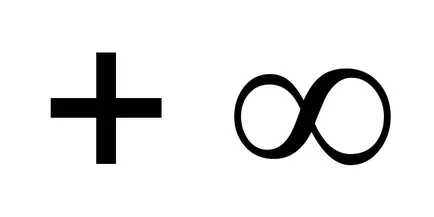

Обърнете се към него по този начин:
ограничение на
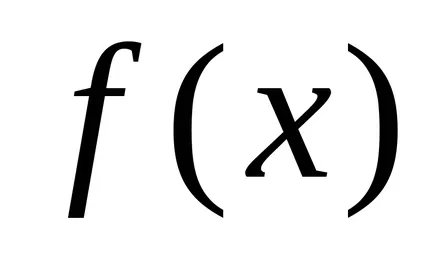
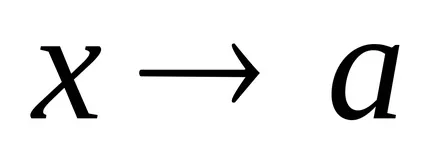
Определение 2. Броят А се нарича граница на функцията
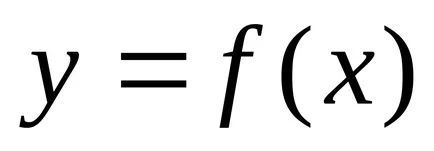
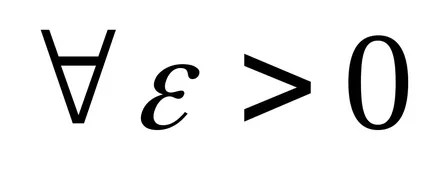
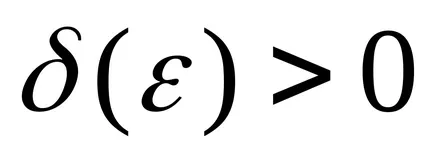
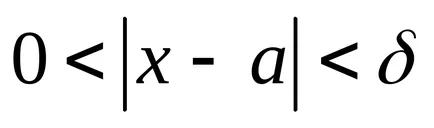
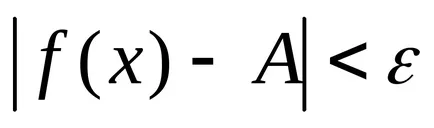
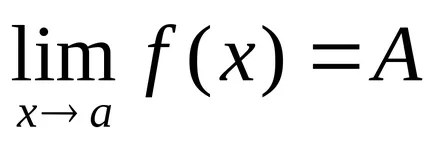
Лесно е да се докаже, че и двете определения са еквивалентни на граничната функция.
Графично определяне на границата, могат да бъдат представени, както следва:
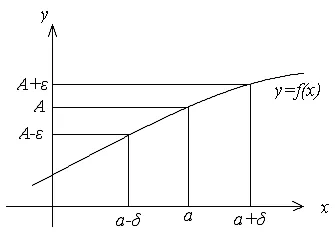
След като аргумент х стойности попадат в


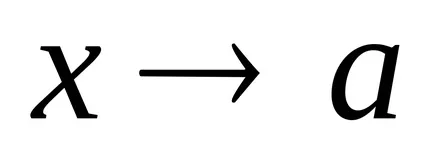
по избор, функция е определен в точка А;


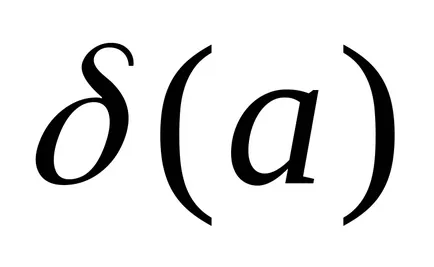
Определение 3. Броят А е граница на функцията