асимптота хипербола

Direct. за който се доближава произволно близо до точка на кривата (клонове на кривата) за нейното движение по крива към безкрайност, хиперболи, наречени асимптота.

Позовавайки се MNKL диагоналите на правоъгълника образуват уравнението на линия ОК (Фигура 22):

директна употреба "лъч" уравнение за подготовката на уравнението. след това.

Пишем уравнението на линията в общия вид:

Ние считаме, разстоянието от точката към линията на хипербола OK, с помощта на формулата изчисляване на разстояние от точката на линия.

Умножете на числителя и знаменателя на фракцията на. получаваме

(. Х0 y0) Тъй M0 - точката на хипербола, неговите координати удовлетворяват уравнението на хипербола (1), след това (виж "The получаването на хипербола."), Тогава:

От тази формула следва, че когато се движат по протежение на хипербола, така че неговите абсцисата Х0 увеличава неопределено (и следователно знаменател от увеличава фракция), след това разстоянието на линията намалява за неопределено време, т.е. - асимптота хипербола.

Същото обстоятелство ще се случи в точка М потоци по хипербола през третото тримесечие (от симетрия за произхода).

И накрая, ние се на втора линия, поради симетрията на хипербола по отношение на оста OY. симетрично разположени права. към която също за неопределено време ще подходи точка M, докато се движат по протежение на хипербола, и на разстояние безкрайност (при втория и четвъртия квадранта).

Тези две линии се наричат ​​асимптоти на хипербола (Фигура 25).

Уравненията на асимптоти на хипербола:

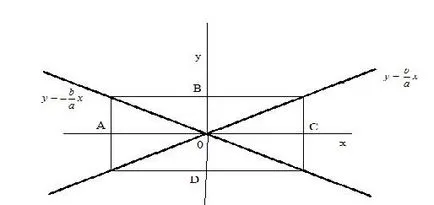
Хипербола асимптоти са разположени по протежение на диагоналите "ядро" хипербола правоъгълник, едната страна на която е успоредна на оста ОХ и равна 2а. друга - успоредно на оста OY и е равна на 2b. а центърът е в основата.

В изграждането на хипербола в уравнението, трябва първо да се изгради своя асимптота.

Изграждане хипербола (фигура 26)

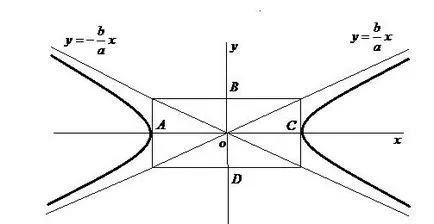
По същия начин, може да се проведе изследване на уравнението (4.2)

и изграждане на хипербола (ФИГУРА 27)